OptimLib: interfaçage d’une bibliothèque C++ d’optimisation, alternative à optim
State of the R
24-28/08/2020
Motivations
- Apprendre à interfacer une librarie C++ avec R en l’intégrant dans un package - Définition des règles de compilation - Utilisation de méthodes d’optimisation alternatives
- Disposer des implémentations alternative des méthodes d’optimisation classiques
- Disposer d’implémentation de méthodes non présentes dans
optim, comme ADAM
La bibliothèque optimLib
Il s’agit d’une bibliothèque C++ développée par Keith O’hara, incluant les algorithmes d’optimisation suivants:
- Broyden’s Method (for root finding)
- Newton’s method, BFGS, and L-BFGS
- Gradient descent: basic, momentum, Adam, AdaMax, Nadam, NadaMax, and more
- Nonlinear Conjugate Gradient
- Nelder-Mead
- Differential Evolution (DE)
- Particle Swarm Optimization (PSO)
L’appel aux algorithmes se fait de la manière suivante en C++
algorithm_name(<initial and final values>, <objective function>, <objective function data>);Réalisation
Nous avons proposé une première version d’un package R optimLibR intégrant de manière minimale la librarie C++
devtools::install_github("StateOfTheR/optimLibR")library(optimLibR)Pour ce faire, le code source de la bibliothèque optimLib est intégré sous forme de “.hpp” (header only") dans le répertoire inst/include du package. Il suffit ensuite de déclarer correctement les variables de compilation dans les fichiers Makevars du répertoire src.
PKG_CXXFLAGS = $(SHLIB_OPENMP_CXXFLAGS) -I../inst/include -DUSE_RCPP_ARMADILLO
PKG_LIBS= $(SHLIB_OPENMP_CXXFLAGS) $(LAPACK_LIBS) $(BLAS_LIBS) $(FLIBS)
CXX_STD = CXX11Tests d’utilisation
Nous avons intégré au package les deux fonctions de tests C+++ proposée par Keith O’hara, placé dans le répertoire src
Ackley function
Consider searching for the global minimum of the Ackley function:
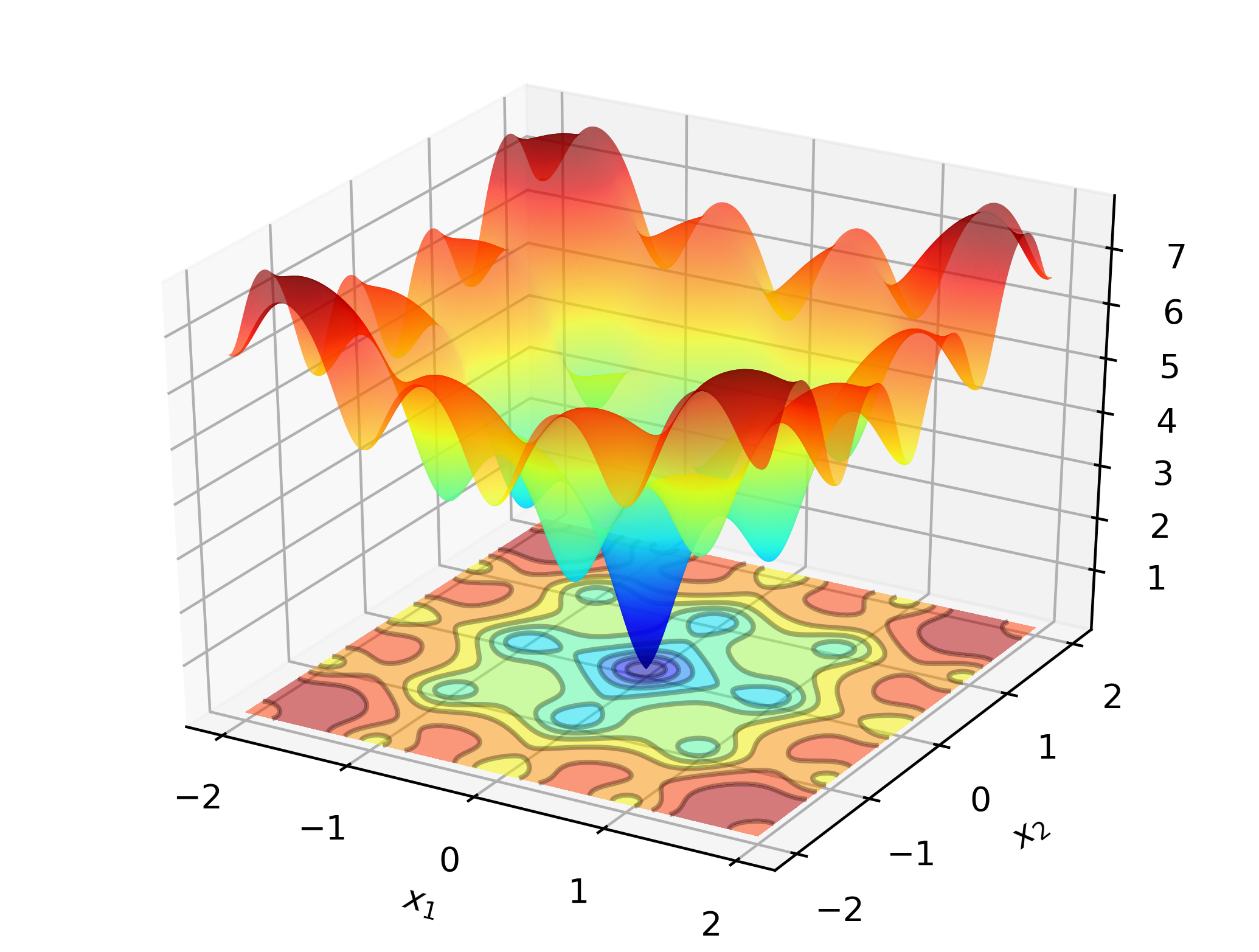
Ackley
This is a well-known test function with many local minima. Newton-type methods (such as BFGS) are sensitive to the choice of initial values, and will perform rather poorly here. As such, we will employ a global search method; in this case: Differential Evolution.
ackley_function()##
## de: solution to Ackley test:
## -2.3970e-16
## -1.4593e-16## [,1]
## [1,] -2.397020e-16
## [2,] -1.459261e-16Avec les méthodes intégrées dans la fonction optim, la qualité de la minimisation est variable, selon la recherche d’un optimum local ou global et du point de départ:
ackley <- function(x0) {
x <- x0[1]
y <- x0[2]
res <- -20*exp( -0.2*sqrt(0.5*(x*x + y*y)) ) - exp( 0.5*(cos(2*pi*x) + cos(2*pi*y)) ) + 20 + exp(1)
res
}
x0 <- c(-1,1)
optim(x0, ackley, method = "Nelder-Mead")$par## [1] -0.9685125 0.9685059optim(x0, ackley, method = "SANN")$par## [1] 1.693916e-05 5.431146e-03optim(x0, ackley, method = "L-BFGS-B")$par## [1] -1.104201e-16 1.104201e-16optim(x0, ackley, method = "BFGS")$par## [1] -0.9684772 0.9684772Logistic regression
For a data-based example, consider maximum likelihood estimation of a logit model, common in statistics and machine learning. In this case we have closed-form expressions for the gradient and hessian. We will employ a popular gradient descent method, Adam (Adaptive Moment Estimation), and compare to a pure Newton-based algorithm.
logit_optimLib()##
## Adam: true values vs estimates:
## 2.9834 2.8992
## 1.5256 1.4851
## 1.8980 1.8649
## 1.6909 1.6968
## 2.9562 2.8573
##
##
## newton: true values vs estimates:
## 2.9834 2.8992
## 1.5256 1.4851
## 1.8980 1.8649
## 1.6909 1.6968
## 2.9562 2.8573## [,1]
## [1,] 2.899163
## [2,] 1.485078
## [3,] 1.864900
## [4,] 1.696774
## [5,] 2.857337TODO / À faire
L’idée serait de développer une interface complète R/C++ avec chacun des algorithme implémenté dans optimLib, à la manière du package nloptr par exemple.