library(distributional)
library(ggplot2)
theme_set(theme_minimal())

Utilisation basique

Création d’une loi normale

dn <- dist_normal(mu = 5, sigma = 2)
dn
## <distribution[1]>
## [1] N(5, 4)
class(dn)
## [1] "distribution" "vctrs_vctr"   "list"

Quelques quantités d’intérêt

list(mean = mean(dn), median = median(dn), variance = variance(dn), 
     skewness = skewness(dn), kurtosis = kurtosis(dn))
## $mean
## [1] 5
## 
## $median
## [1] 5
## 
## $variance
## [1] 4
## 
## $skewness
## [1] 0
## 
## $kurtosis
## [1] 0

Courbes

autoplot(dn)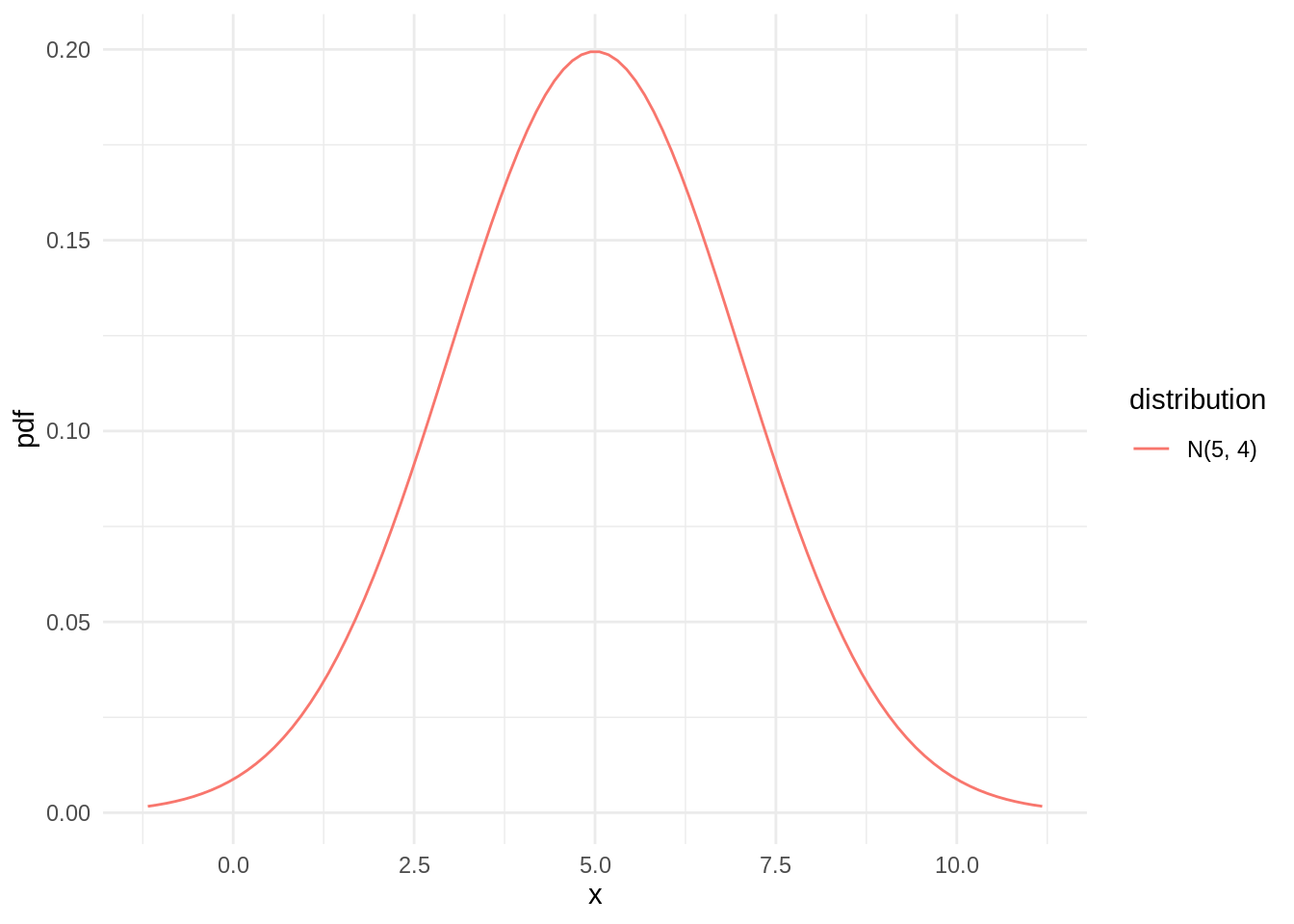

Intervalles

hilo(dn) # intervalle de confiance
## <hilo[1]>
## [1] [1.080072, 8.919928]95
hdr(dn) # intervalle du ou des modes
## <list_of<hilo>[1]>
## [[1]]
## <hilo[1]>
## [1] [4.872133, 5.127867]95

Échantillonage

sample <- generate(dn, times = 10)
sample
## [[1]]
##  [1] 8.7327414 4.4217227 4.0222503 5.1959268 0.8604043 8.7733245 3.9748876
##  [8] 4.0265389 3.5023046 3.6806334
likelihood(dn, sample)
## [1] 1.387716e-10
cdf(dn, 5)
## [1] 0.5
quantile(dn, 0.5)
## [1] 5

Calculs

2 * dn - 5 
## <distribution[1]>
## [1] N(5, 16)
dn ^ 2 # ne connait pas
## <distribution[1]>
## [1] t(N(5, 4))

Vecteur de distribution

dchi <- dist_chisq(df = 5)
dt <- dist_student_t(df = 10)
dm <- dist_mixture(dt, dn, weights = c(0.6, 0.4))
dvec <- c(dn, dchi, dt, dm)
dvec
## <distribution[4]>
## [1] N(5, 4)      ᵪ²(5)        t(10, 0, 1)  mixture(n=2)
autoplot(dvec)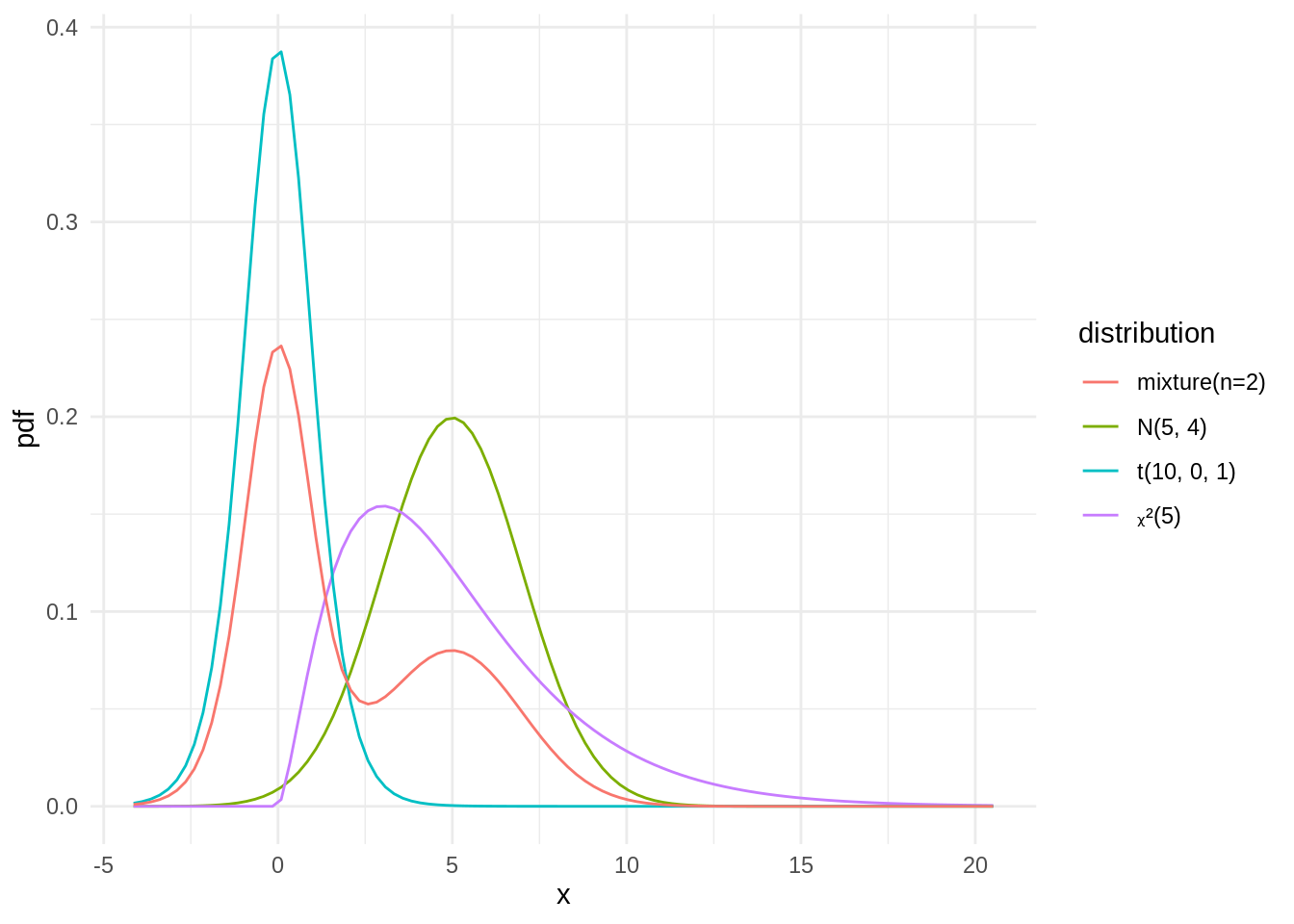

mean(dvec)
## [1] 5 5 0 2
variance(dvec)
## [1]  4.00 10.00  1.25  8.35
hilo(dvec, size = 66)
## <hilo[4]>
## [1] [ 3.0916695, 6.908331]66 [ 2.1361740, 7.759460]66 [-1.0019404, 1.001940]66
## [4] [-0.5978206, 5.379412]66
cdf(dvec, 5)
## [1] 0.5000000 0.5841198 0.9997313 0.7998388

Graphiques

library(ggdist)
df <- data.frame(name = factor(c("N(5,4)", "\u1d6a²(5)", "t(10, 0, 1)", "Mixture"), 
                               levels = c("N(5,4)", "\u1d6a²(5)", "t(10, 0, 1)", "Mixture")),
                 dist = dvec)
df
##          name         dist
## 1      N(5,4)      N(5, 4)
## 2       ᵪ²(5)        ᵪ²(5)
## 3 t(10, 0, 1)  t(10, 0, 1)
## 4     Mixture mixture(n=2)
ggplot(df) +
  aes(y = name, dist = dist, fill = name) +
  stat_dist_halfeye(show.legend = FALSE, .width = c(0.66, 0.95)) +
  labs(x = NULL, y = NULL)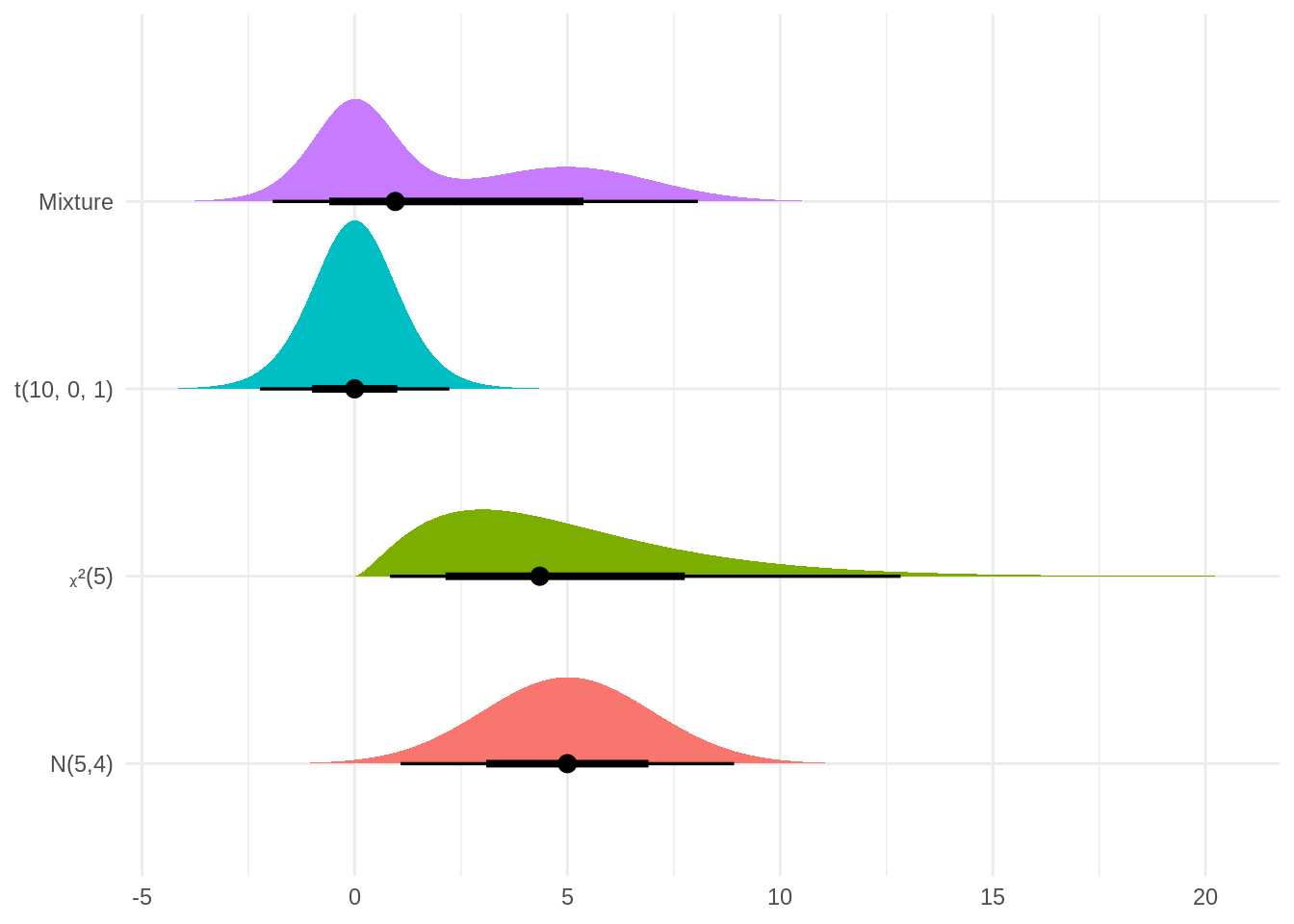

ggplot(df) +
  aes(y = name, dist = dist, fill = name) +
  stat_dist_gradientinterval(show.legend = FALSE) +
  labs(x = NULL, y = NULL)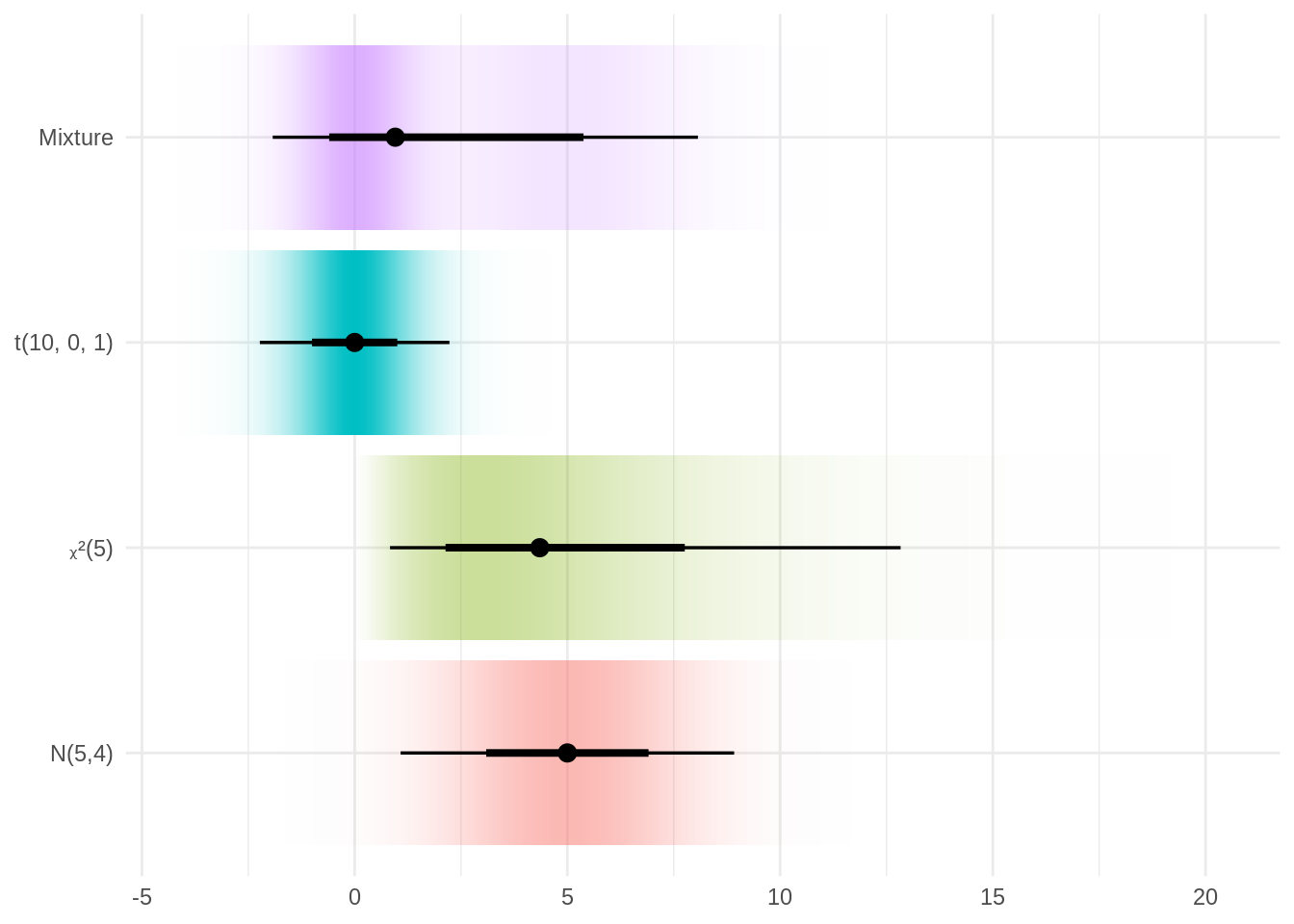

ggplot(df) +
  aes(y = name, dist = dist, fill = name) +
  stat_dist_dots(quantiles = 150, show.legend = FALSE) +
  labs(x = NULL, y = NULL)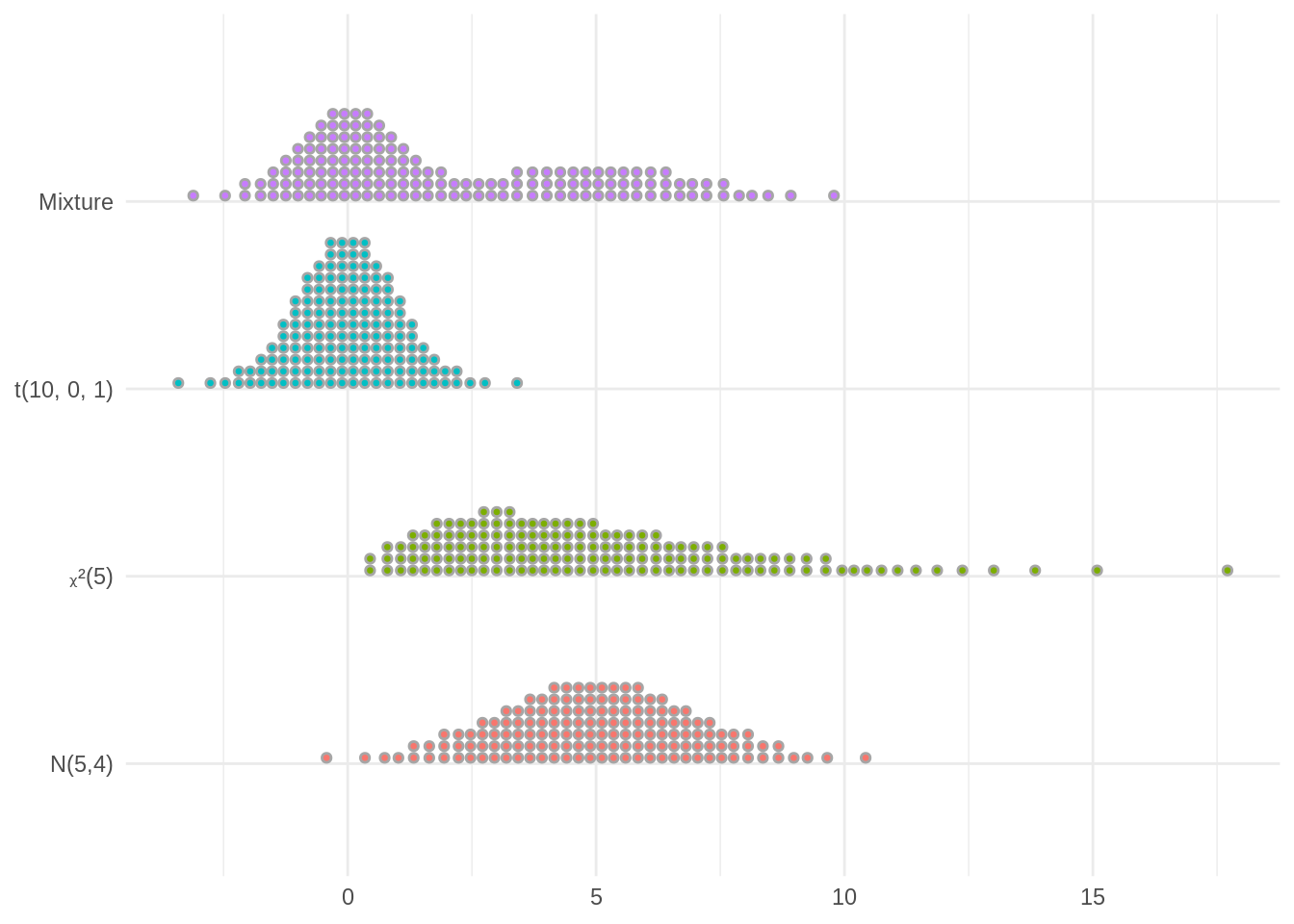

Lois discretes

dp <- dist_poisson(4)
dp
## <distribution[1]>
## [1] Pois(4)
mean(dp)
## [1] 4
generate(dp, 10)
## [[1]]
##  [1] 5 2 4 1 1 8 2 5 7 1

Loi inflatée

dpi <- dist_inflated(dp, 0.5, x = 0)
dpi
## <distribution[1]>
## [1] 0+Pois(4)
mean(dpi)
## [1] 2
generate(dpi, 10)
## [[1]]
##  [1] 6 7 0 0 0 2 0 2 0 2

Distribution disponibles

ls("package:distributional", pattern = "^dist_")
##  [1] "dist_bernoulli"                "dist_beta"                    
##  [3] "dist_binomial"                 "dist_burr"                    
##  [5] "dist_cauchy"                   "dist_chisq"                   
##  [7] "dist_degenerate"               "dist_exponential"             
##  [9] "dist_f"                        "dist_gamma"                   
## [11] "dist_geometric"                "dist_gumbel"                  
## [13] "dist_hypergeometric"           "dist_inflated"                
## [15] "dist_inverse_exponential"      "dist_inverse_gamma"           
## [17] "dist_inverse_gaussian"         "dist_logarithmic"             
## [19] "dist_logistic"                 "dist_mixture"                 
## [21] "dist_multinomial"              "dist_multivariate_normal"     
## [23] "dist_negative_binomial"        "dist_normal"                  
## [25] "dist_pareto"                   "dist_percentile"              
## [27] "dist_poisson"                  "dist_poisson_inverse_gaussian"
## [29] "dist_sample"                   "dist_student_t"               
## [31] "dist_studentized_range"        "dist_transformed"             
## [33] "dist_truncated"                "dist_uniform"                 
## [35] "dist_weibull"                  "dist_wrap"