Binder

Références

Dans son livre, Generalized Additive Models, An Introduction with R, S. Wood commence par des rappels sur les modèles de régression linéaire simples et les GLM avant de présenter les modèles additifs généralisés (GAM) et différentes bases de splines ainsi que leur utilisation. Le livre coexiste avec le package R mgcv que nous avons utilisé dans la suite.

Une formation GAM en R est disponible sur le site RStudio Education et utilise également le package mgcv.

Modèles additifs généralisés

Un modèle additif généralisé est un GLM dans lequel le prédicteur linéaire fait intervenir une somme de fonctions régulières des covariables. Les modèles additifs généralisés ont une structure de la forme suivante \[g(\mu_i)=A_i\theta+\sum_j f_j(x_{ji}),\, Y_i\sim\text{EF}(\mu_i,\phi)\] où \(Y_i\) est la variable réponse et \(\text{EF}(\mu_i,\phi)\) est une distribution de famille exponentielle de moyenne \(\mu_i\) et de paramètre d’échelle \(\phi\) et \(A_i\theta\) représente une componente paramétrique dans la modélisation.

Pour estimer les \(f_j\), on les décompose sur une base de splines. On note \(b_{jk}(x)\) la \(k\)ème fonction de la base de splines choisie, on suppose que \(f_j\) s’écrit \[f_j(x)=\sum_{k=1}^l b_{jk}(x)\beta_{jk},\] avec \(\beta_{jk}\) inconnu.

Base de splines

On veut construire une base de \(k\) fonctions splines \((s_1, \ldots, s_k)\). Pour ceci, on définit \(k\) nuds, par défaut les extrémités correspondent à \(x_{min}\) et \(x_{max}\).

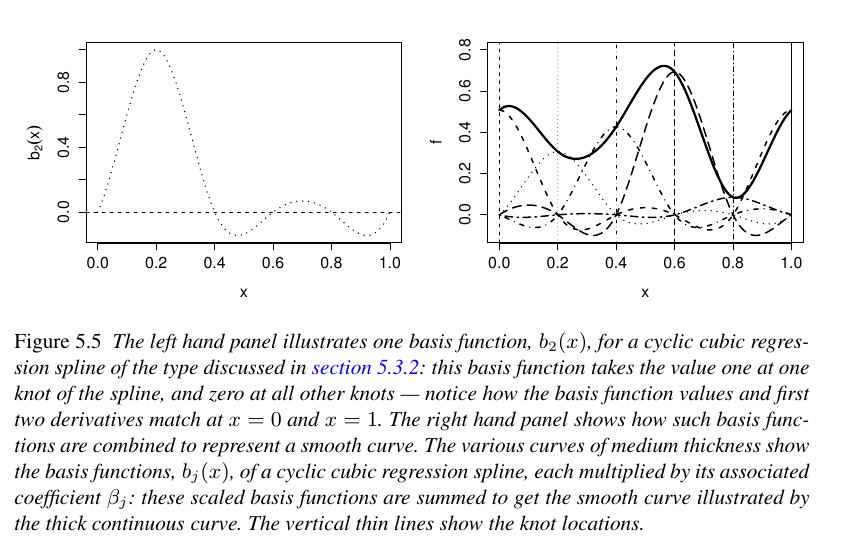
Chaque fonction \(s_i\) vaut 1 au noeud \(i\) et \(0\) aux autres nuds. En outre. Chaque fonction spline (cubique) est le recollement de \(k\) polynomes de degré 3 assurant une fonction de classe \(C^2\) sur l’intervalle, comme illustré ci-dessous (extrait du livre de S. Wood).

library(mgcv)
## Loading required package: nlme
## 
## Attaching package: 'nlme'
## The following object is masked from 'package:dplyr':
## 
##     collapse
## This is mgcv 1.8-33. For overview type 'help("mgcv-package")'.
library(tidyverse)
library(MASS)
## 
## Attaching package: 'MASS'
## The following object is masked from 'package:dplyr':
## 
##     select
Mods3 <- gam(accel~s(times,k=10,bs="cr"),data=mcycle)
gam.check(Mods3)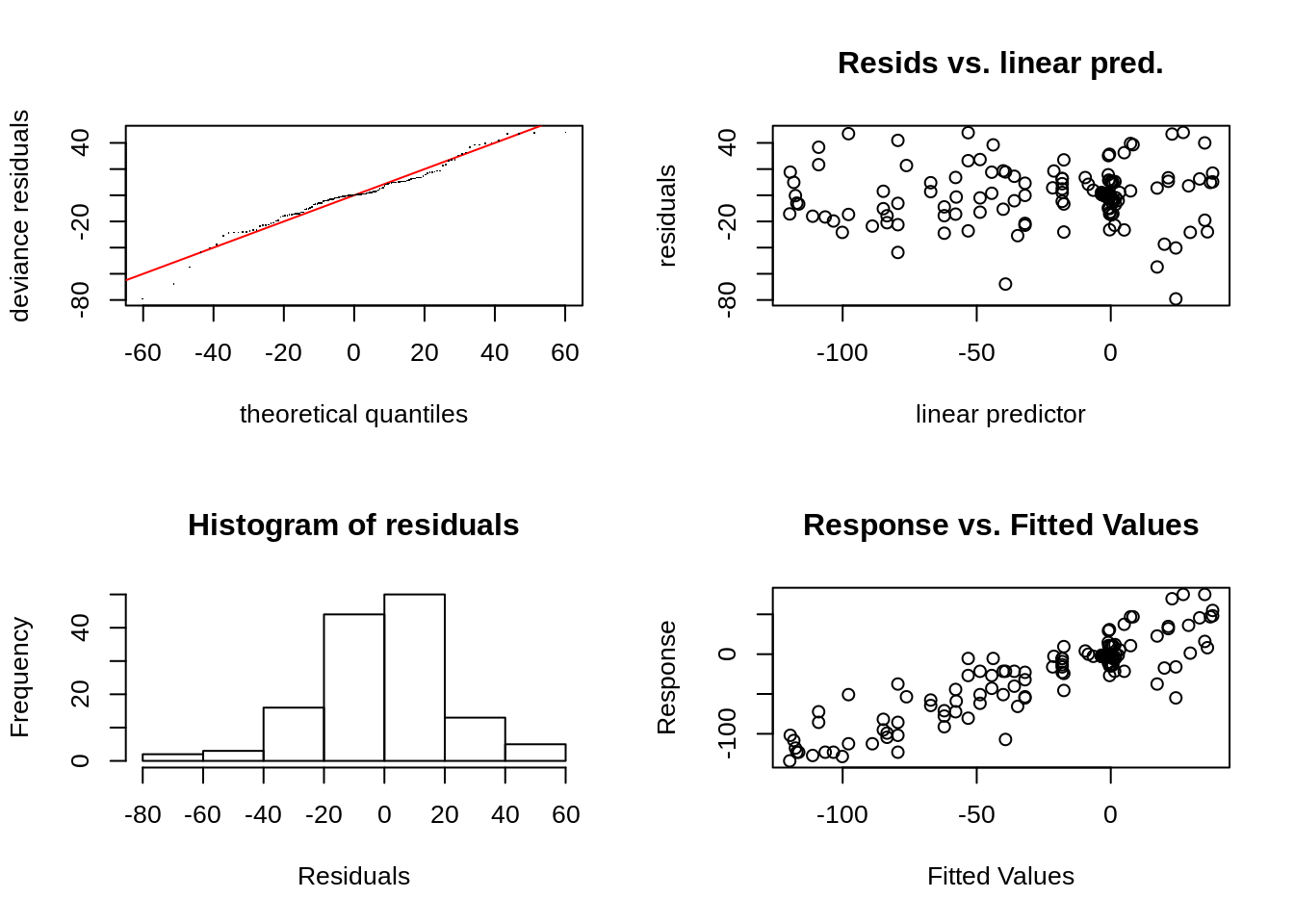

## 
## Method: GCV   Optimizer: magic
## Smoothing parameter selection converged after 8 iterations.
## The RMS GCV score gradient at convergence was 0.0002188377 .
## The Hessian was positive definite.
## Model rank =  10 / 10 
## 
## Basis dimension (k) checking results. Low p-value (k-index<1) may
## indicate that k is too low, especially if edf is close to k'.
## 
##            k'  edf k-index p-value
## s(times) 9.00 8.39    1.15    0.95
summary(Mods3)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## accel ~ s(times, k = 10, bs = "cr")
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  -25.546      1.951   -13.1   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##           edf Ref.df     F p-value    
## s(times) 8.39  8.867 53.84  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.783   Deviance explained = 79.7%
## GCV = 544.48  Scale est. = 506.04    n = 133

\[Y_i = Z_i^T\theta + \sum_{j=1}^p \beta_j f_j(x_{i}) + \epsilon_i\] où les \(f_j\) forment une base de spline, \(Z_i\) des variables utilisées comme dans un modèle linéaire, et \(x_i\) la variable pour laquelle on utilise une spline. Notons qu’on peut avoir des splines multivariés et plusieurs splines dépendant de différentes variables.

Dans le tableau, Parametric Coefficients correspond à la partie des effets linéaires et la partie smooth terms correspond au test sur la variable dont dépend le spline.

La dernière partie contient des informations sur la qualité d’ajustement du modèle type \(R^2\) et variance estimée.

Ce tableau contient les \(\beta_j\) devant les splines :

coef(Mods3)
## (Intercept)  s(times).1  s(times).2  s(times).3  s(times).4  s(times).5 
##   -25.54586    17.79652    -5.19623   -68.18822   -93.55637   -19.17075 
##  s(times).6  s(times).7  s(times).8  s(times).9 
##    55.62357    32.75658    16.34183    23.85845

Autres références :