See Chapter 9 in Convex Optimization

http://:web.stanford.edu/~boyd/cvxbook/

Online courses

All slides stolen (extracted/re-arranged) from :

• Convex Optimization: http://www.seas.ucla.edu/~vandenbe/ee236b/ee236b.html
• Optimization Methods for Large-Scale Systems http://www.seas.ucla.edu/~vandenbe/ee236c/ee236c.html

Rosenbrock Banana function

\[ f(x) = 100( x_2 - x_2^2) + (1-x_1)^2 \]

\[ \nabla f (x) = \begin{pmatrix} -400 x_1 (x_2 - x_1^2) - 2 (1-x_1) \\ 200 (x_2 - x_1^2) \end{pmatrix} \]

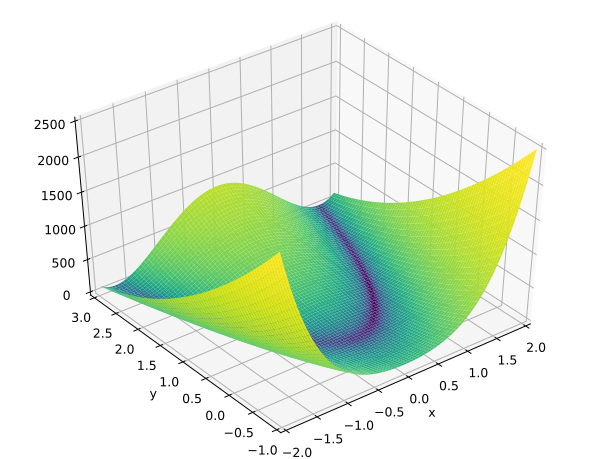
Rosenbrock Banana function in R

objective <- function(x) {
  return( 100 * (x[2] - x[1] * x[1])^2 + (1 - x[1])^2 )
}

gradient <- function(x) {
  return( c( -400 * x[1] * (x[2] - x[1] * x[1]) - 2 * (1 - x[1]), 200 * (x[2] - x[1] * x[1]) ) )
}

optim usage

optim(par, fn, gr = NULL, ...,
      method = c("Nelder-Mead", "BFGS", "CG", "L-BFGS-B", "SANN",
                 "Brent"),
      lower = -Inf, upper = Inf,
      control = list(), hessian = FALSE)

Call to optim - BFGS

x0 <- c(-1.2, 1)
res_bfgs <- optim(x0, objective, gradient, method = "BFGS", control= list(trace = 2))

## initial  value 24.200000 
## iter  10 value 1.367383
## iter  20 value 0.134560
## iter  30 value 0.001978
## iter  40 value 0.000000
## final  value 0.000000 
## converged

Call to optim - CG

x0 <- c(-1.2, 1)
res_cg <- optim(x0, objective, gradient, method = "CG", control= list(trace = 2))

##   Conjugate gradients function minimizer
## Method: Fletcher Reeves
## tolerance used in gradient test=3.63798e-12
## 0 1 24.200000
## parameters   -1.20000    1.00000 
## **** i< 1 7 4.132161
## parameters   -1.02752    1.07040 
## * i> 2 10 4.126910
## parameters   -1.02855    1.06882 
## **** i> 3 16 4.121409
## parameters   -1.02924    1.06533 
##  i> 4 18 4.106523
## parameters   -1.02586    1.05731 
## **** i> 5 24 4.100955
## parameters   -1.02261    1.05573 
##  i> 6 26 4.086136
## parameters   -1.01839    1.04818 
## **** i> 7 32 4.080524
## parameters   -1.01914    1.04464 
##  i> 8 34 4.065787
## parameters   -1.01579    1.03670 
## **** i> 9 40 4.060127
## parameters   -1.01250    1.03514 
##  i> 10 42 4.045415
## parameters   -1.00824    1.02768 
## **** i> 11 48 4.039717
## parameters   -1.00900    1.02412 
##  i> 12 50 4.025073
## parameters   -1.00568    1.01621 
## **** i> 13 56 4.019328
## parameters   -1.00236    1.01467 
##  i> 14 58 4.004703
## parameters   -0.99804    1.00728 
## **** i> 15 64 3.998920
## parameters   -0.99880    1.00370 
##  i> 16 66 3.984360
## parameters   -0.99552    0.99582 
## **** i> 17 72 3.978528
## parameters   -0.99217    0.99429 
##  i> 18 74 3.963986
## parameters   -0.98779    0.98699 
## **** i> 19 80 3.958118
## parameters   -0.98855    0.98339 
##  i> 20 82 3.943639
## parameters   -0.98530    0.97553 
## **** i> 21 88 3.937719
## parameters   -0.98192    0.97402 
##  i> 22 90 3.923256
## parameters   -0.97749    0.96680 
## **** i> 23 96 3.917299
## parameters   -0.97824    0.96317 
##  i> 24 98 3.902898
## parameters   -0.97502    0.95534 
## **** i> 25 104 3.896888
## parameters   -0.97161    0.95384 
##  i> 26 106 3.882502
## parameters   -0.96712    0.94670 
## **** i> 27 112 3.876454
## parameters   -0.96787    0.94306 
##  i> 28 114 3.862128
## parameters   -0.96469    0.93524 
## **** i> 29 120 3.856025
## parameters   -0.96125    0.93376 
##  i> 30 122 3.841712
## parameters   -0.95669    0.92669 
## **** i> 31 128 3.835572
## parameters   -0.95743    0.92303 
##  i> 32 130 3.821316
## parameters   -0.95429    0.91522 
## **** i> 33 136 3.815119
## parameters   -0.95082    0.91376 
##  i> 34 138 3.800875
## parameters   -0.94618    0.90677 
## **** i> 35 144 3.794641
## parameters   -0.94692    0.90309 
##  i> 36 146 3.780452
## parameters   -0.94382    0.89530 
## **** i> 37 152 3.774158
## parameters   -0.94032    0.89385 
##  i> 38 154 3.759979
## parameters   -0.93561    0.88694 
## **** i> 39 160 3.753649
## parameters   -0.93635    0.88323 
##  i> 40 162 3.739522
## parameters   -0.93327    0.87545 
## **** i> 41 168 3.733129
## parameters   -0.92975    0.87402 
##  i> 42 170 3.719010
## parameters   -0.92496    0.86719 
## **** i> 43 176 3.712582
## parameters   -0.92569    0.86346 
##  i> 44 178 3.698513
## parameters   -0.92265    0.85568 
## **** i> 45 184 3.692020
## parameters   -0.91909    0.85427 
##  i> 46 186 3.677956
## parameters   -0.91422    0.84751 
## **** i> 47 192 3.671429
## parameters   -0.91495    0.84377 
##  i> 48 194 3.657411
## parameters   -0.91194    0.83598 
## **** i> 49 200 3.650816
## parameters   -0.90836    0.83459 
##  i> 50 202 3.636803
## parameters   -0.90340    0.82791 
## **** i> 51 208 3.630174
## parameters   -0.90412    0.82414 
##  i> 52 210 3.616203
## parameters   -0.90115    0.81636 
## **** i> 53 216 3.609503
## parameters   -0.89754    0.81498 
##  i> 54 218 3.595534
## parameters   -0.89249    0.80838 
## **** i> 55 224 3.588802
## parameters   -0.89320    0.80459 
##  i> 56 226 3.574871
## parameters   -0.89026    0.79679 
## **** i> 57 232 3.568067
## parameters   -0.88662    0.79544 
##  i> 58 234 3.554135
## parameters   -0.88148    0.78891 
## **** i> 59 240 3.547298
## parameters   -0.88217    0.78510 
##  i> 60 242 3.533401
## parameters   -0.87927    0.77729 
## **** i> 61 248 3.526489
## parameters   -0.87561    0.77595 
##  i> 62 250 3.512588
## parameters   -0.87036    0.76950 
## **** i> 63 256 3.505645
## parameters   -0.87105    0.76567 
##  i> 64 258 3.491774
## parameters   -0.86818    0.75784 
## **** i> 65 264 3.484754
## parameters   -0.86448    0.75653 
##  i> 66 266 3.470875
## parameters   -0.85914    0.75015 
## **** i> 67 272 3.463826
## parameters   -0.85981    0.74630 
##  i> 68 274 3.449973
## parameters   -0.85697    0.73845 
## **** i> 69 280 3.442843
## parameters   -0.85325    0.73715 
##  i> 70 282 3.428978
## parameters   -0.84779    0.73085 
## **** i> 71 288 3.421820
## parameters   -0.84844    0.72698 
##  i> 72 290 3.407976
## parameters   -0.84564    0.71910 
## **** i> 73 296 3.400736
## parameters   -0.84189    0.71782 
##  i> 74 298 3.386876
## parameters   -0.83632    0.71160 
## **** i> 75 304 3.379609
## parameters   -0.83696    0.70771 
##  i> 76 306 3.365764
## parameters   -0.83418    0.69979 
## **** i> 77 312 3.358412
## parameters   -0.83041    0.69853 
##  i> 78 314 3.344546
## parameters   -0.82472    0.69239 
## **** i> 79 320 3.337170
## parameters   -0.82533    0.68848 
##  i> 80 322 3.323313
## parameters   -0.82258    0.68052 
## **** i> 81 328 3.315850
## parameters   -0.81879    0.67928 
##  i> 82 330 3.301967
## parameters   -0.81297    0.67321 
## **** i> 83 336 3.294481
## parameters   -0.81356    0.66928 
##  i> 84 338 3.280600
## parameters   -0.81084    0.66128 
## **** i> 85 344 3.273027
## parameters   -0.80703    0.66006 
##  i> 86 346 3.259113
## parameters   -0.80108    0.65407 
## **** i> 87 352 3.251518
## parameters   -0.80164    0.65012 
##  i> 88 354 3.237599
## parameters   -0.79894    0.64206 
## **** i> 89 360 3.229915
## parameters   -0.79510    0.64086 
##  i> 90 362 3.215957
## parameters   -0.78902    0.63495 
## **** i> 91 368 3.208254
## parameters   -0.78955    0.63098 
##  i> 92 370 3.194282
## parameters   -0.78687    0.62287 
## **** i> 93 376 3.186489
## parameters   -0.78302    0.62168 
##  i> 94 378 3.172470
## parameters   -0.77678    0.61585 
## **** i> 95 384 3.164660
## parameters   -0.77729    0.61186 
##  i> 96 386 3.150619
## parameters   -0.77463    0.60368 
## **** i> 97 392 3.142719
## parameters   -0.77075    0.60252 
##  i> 98 394 3.128622
## parameters   -0.76437    0.59676 
## **** i> 99 400 3.120708
## parameters   -0.76484    0.59276 
##  i> 100 402 3.106579
## parameters   -0.76218    0.58451

nloptr usage

nloptr(x0, eval_f, eval_grad_f, ..., opts = list())

Call to nloptr - BFGS

library(nloptr)
opts <- list("algorithm"="NLOPT_LD_LBFGS", "xtol_rel"=1.0e-8)
res <- nloptr(x0=x0, eval_f=objective, eval_grad_f=gradient, opts=opts)
print(res)

## 
## Call:
## 
## nloptr(x0 = x0, eval_f = objective, eval_grad_f = gradient, opts = opts)
## 
## 
## Minimization using NLopt version 2.4.2 
## 
## NLopt solver status: 1 ( NLOPT_SUCCESS: Generic success return value. )
## 
## Number of Iterations....: 56 
## Termination conditions:  xtol_rel: 1e-08 
## Number of inequality constraints:  0 
## Number of equality constraints:    0 
## Optimal value of objective function:  7.35727226897802e-23 
## Optimal value of controls: 1 1