Torch & Rcpp

Auteur·rice·s

Annaig De-Walsche

Barbara Bricout

Tristan Mary-Huard

Armand Favrot

Félix Cheysson

Théodore Vanrenterghem

Date de publication

8 août 2024

library(Rcpp)
library(RcppArmadillo)
library(torch)
library(tictoc)
library(bench) # comparaison des vitesses
library(ggplot2)
library(ggbeeswarm)

Torch on R

La librairie {torch} de R permet la manipulation de tenseur en R. Elle permet notamment de faire la différenciation automatique, c-a-d d’évaluer numériquement le gradient d’une fonction et d’effectuer des descentes de gradient.

Présentation finistR2022

Torch and Automatic differentiation

Rcpp

L’utilisation de {Rcpp} permet d’exporter des fonctions C++ en R. Les fonctions seront alors directement utilisables dans un script et avec des arguments R. Ainsi on peut tirer partie de la compilation d’un code C++, et accélérer de nombreux calculs algébriques.

Pour le calcul algébrique il est utile d’intégrer le package {RcppArmadillo} qui donne accès à la librairie {Armadillo} de C++ lorsque l’on appel une fonction {Rcpp} dans R.

Présentation finistR2018

Example

Dans cet exemple nous allons calculer la perte d’une fonction logistique en R et en C++. Puis comparer les résultats avec le package {bench} de R.

Coder la fonction en C++

// [[Rcpp::depends(RcppArmadillo)]]
#include <RcppArmadillo.h>

// Logistic loss
// [[Rcpp::export]]
// const : pas de changement de valeur dans la fonction
// arma:: : se sont les classes de Armadillo
// using namespace arma to erase all arma::
// & :  appel sans copie donc plus rapide
double loss_cpp( const arma::vec theta, const arma::vec& y, const arma::mat& x ) {
  arma::vec odds(x.n_rows);
  odds = x * theta;
  double log_lik;
  log_lik = arma::dot(y, odds) - arma::sum(arma::log(1 + arma::exp(odds)));
  return(-log_lik);
}

Appel et compilation du script depuis R avec la fonction sourceCpp() de {Rcpp}

sourceCpp(file = "logisticloss.cpp")

Fonction loss en R

loss_R <- function(theta, y, x) {
  odds <- x %*% theta
  log_lik <- sum(y * odds - log(1 + exp(odds)))
  return(-as.numeric(log_lik))
}

Résultats

On remarque que les résultats sont identiques pour la fonction {Rcpp} et la fonction en R.

theta = c(0.5, 0.1)
y = 1.0
x = matrix(c(0.1, 0.2), 1, 2)
loss_cpp(theta, y, x)
[1] 0.6587596
loss_R(theta, y, x)
[1] 0.6587596

Dans l’optique de comparer les performances de ces deux fonctions on utilise la fonction mark() du package {bench}.

n_covar <- 300
size <- 1000

theta <- rnorm(n_covar)
y <- as.numeric(rbinom(size, 1, 0.3))
x <- matrix(rnorm(size * n_covar), size, n_covar)
comp_tbl <- bench::mark(
  loss_R(theta = theta, y = y, x = x),
  loss_cpp(theta = theta, y = y, x = x),
  iterations = 1000
)

autoplot(comp_tbl)
Loading required namespace: tidyr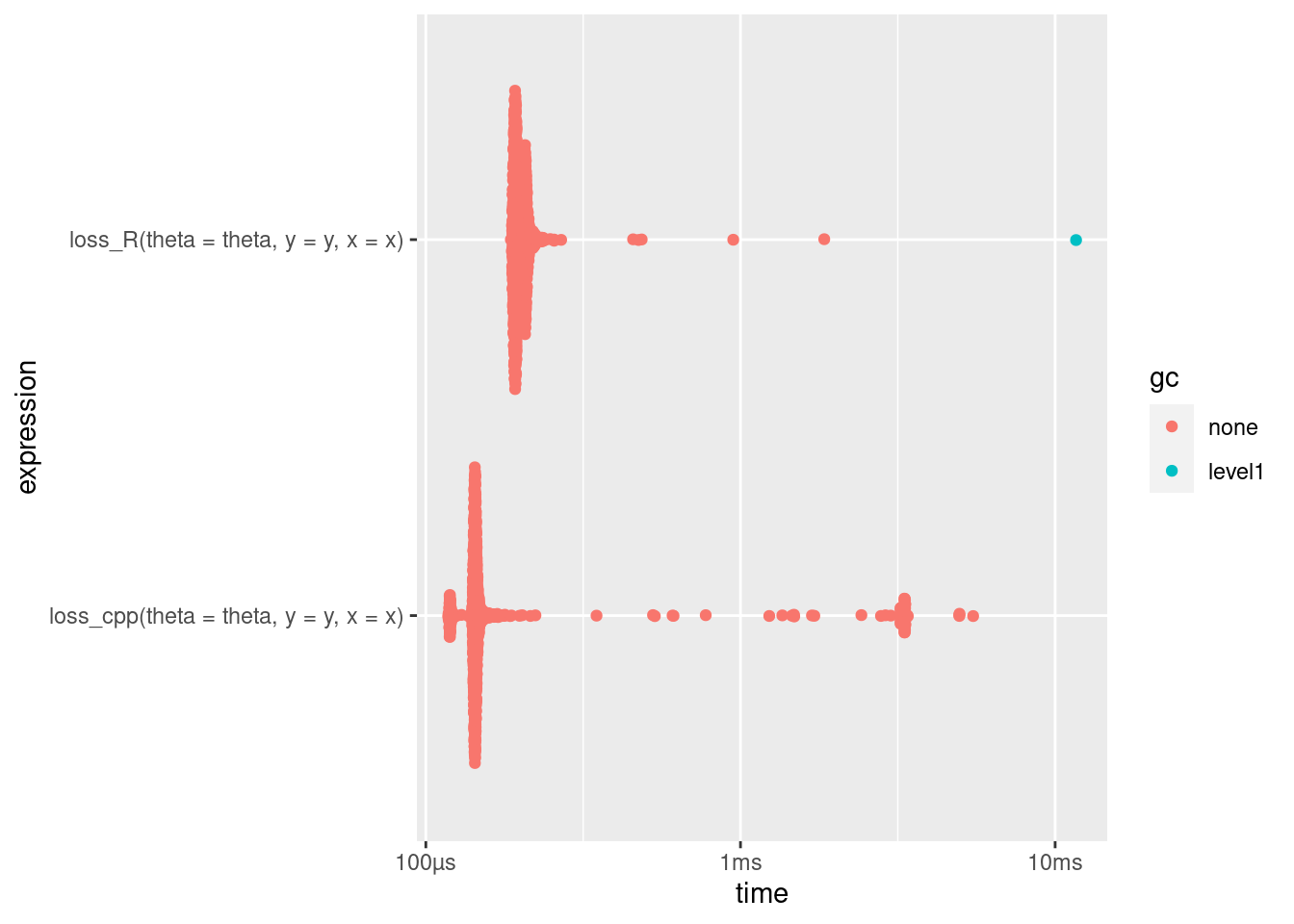

Comme on peut le voir sur le graphique plus haut la fonction loss_cpp() est environ 2 fois plus efficace que la fonction loss_R().

Attention aux librairies BLAS et LAPACK

La librairie BLAS de OpenBlas présentée lors de cette même session ne fonctionne pas correctement avec {Rcpp}. On observe une baisse de fonctionnement très quantitative (facteur 100). La librairie BLAS de Intel MKL reste quant à elle plus efficace.

Références