Comparaison de l’efficatité de R et Julia en Geostatistiques

L’objectif est de comparer des packages R, et Julia pour du krigeage.

On va utiliser :

- R : gstat

- R : GeoModels

- Julia : GeoStats

On compare les points suivant :

- simplicité des données d’entrée

- concision du code

- vitesse d’exécution

- type d’estimation

Pour chaque package, on calculera pour les mêmes données le variogramme empirique, puis on ajustera un variogramme théorique et on fera un krigeage.

Données

library(sp)
library(sf)
library(terra)
data(meuse)
data(meuse.grid)

library(tidyverse)
library(gstat)
library(GeoModels)

On utilise les données meuse du package sp. Celles-ci contiennent des données de concentration en métaux près de la meuse, avec des coordonnées cartésiennes en m.

Pour travailler sur ces concentrations, on passera tout au log afin de les normaliser.

Pour la visualisation en R, on utilise le package terra.

0 - Le package terra

• dernière version : 1.7-39 du 22/06/2023

• Travail des données spatiales sous 2 formes : raster et vector.

  • raster = grilles rectangulaires, adapté aux données continues -> Classe SpatRaster

  • vector = points, lignes, polygones = données discrètes. -> classe SpatVector

• Début de la doc = récap des méthodes importantes (il faut bien, la doc fait 300 pages)

• Sert à manipuler, visualiser des objets spatiaux, notamment après les calculs pour simplifier le travail sur les résultats.

Méthode rast = créer un objet de classe SpatRaster. Le type de la 1ere entrée peut varier.

meuseRast = rast(meuse.grid,type="xyz",crs = "EPSG:2154")
meuseVect = vect(meuse,geom=(c('x','y')))

meuseRastCd = rast(select(meuse,x,y,zinc),type="xyz")
log(meuseRastCd)

class       : SpatRaster 
dimensions  : 3898, 2786, 1  (nrow, ncol, nlyr)
resolution  : 1, 1  (x, y)
extent      : 178604.5, 181390.5, 329713.5, 333611.5  (xmin, xmax, ymin, ymax)
coord. ref. :  
source(s)   : memory
name        :     zinc 
min value   : 4.727388 
max value   : 7.516977 

meuseRastCu = rast(select(meuse,x,y,copper),type="xyz")
meuseRastCuCd = c(meuseRastCd,meuseRastCd) #methode c() = combinaison de layers

1 - Package R gstat

gstat est disponible sur le CRAN : https://CRAN.R-project.org/package=gstat

On peut y trouver également un tutoriel sur le dataset “meuse” utilisé ici, qui présentent le type de données spatiales utilisées par le package (spatial dataframe, données grillées) et les méthodes permettant de travailler avec (méthodes de visualisation du package sp, ajustement de variogrammes, directionnels ou non, krigeage, simulation conditionnelle).

La version la plus ancienne sur les archives du CRAN date de 2003.

Au départ, les données spatiales supportées étaient celles du package sp, mais les données de type sf le sont également.

INSERER AU BON ENDROIT LES CELLULES

Transformation au format sf

df = select(meuse,x,y,cadmium,zinc)
df_grid = select(meuse.grid,x,y)
df_sf <- df %>% 
  sf::st_as_sf( coords = c('x','y'))

df_sf <- sf::st_make_valid(df_sf)
df_grid_sf = df_grid%>% sf::st_as_sf(coords = c('x','y'))%>%sf::st_make_valid()
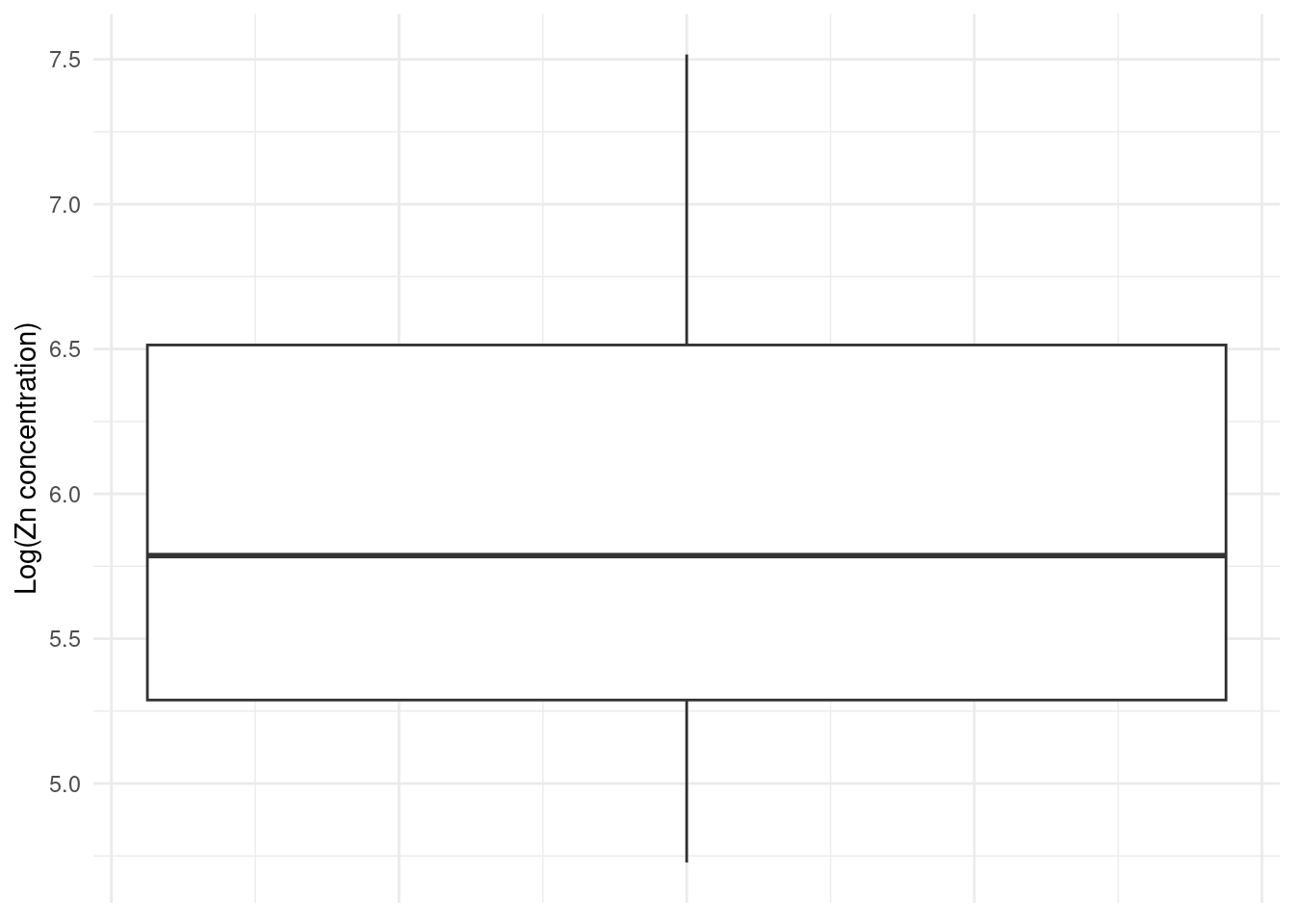
ggplot(df, aes(y=log(zinc))) + 
  geom_boxplot(notch=FALSE) +
  labs(y = "Log(Zn concentration)") +
  theme_minimal() +                                   
  theme(
    axis.text.x = element_blank(),
    axis.ticks = element_blank(),
    axis.line = element_blank()
  )

Variogramme empirique

Pour simplifier la comparaison avec le package Julia, on va se contenter d’une moyenne constante sans introduire de prédicteurs : on demande donc log(zinc)~1. Si on avait voulu, comme dans le tutoriel du package, expliquer la moyenne par la distance à la rivière, il faudrait modifier cette formule en log(zinc)~distance après avoir rajouté une colonne distance au sf dataframe.

Appeler plot sur un objet issu de variogram permet d’en obtenir un tracé.

start_time <- Sys.time()
test <- variogram(log(zinc)~1  , df_sf,cutoff = 2000)
end_time <- Sys.time()
end_time - start_time

Time difference of 0.02656889 secs

plot(test)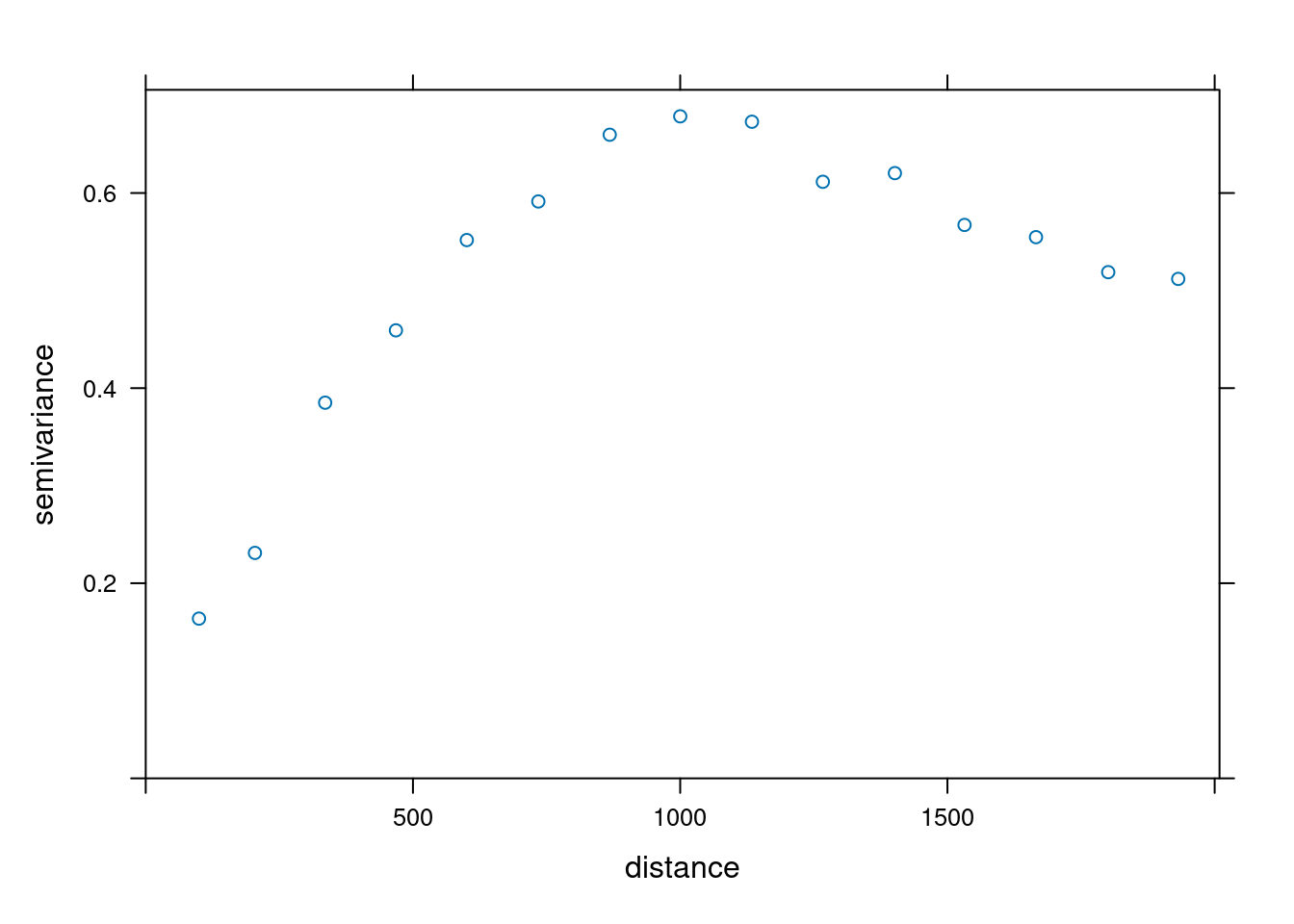

Le type vgm

Plusieurs modèles de variogrammes spatiaux sont disponibles dans la librairie.

show.vgms()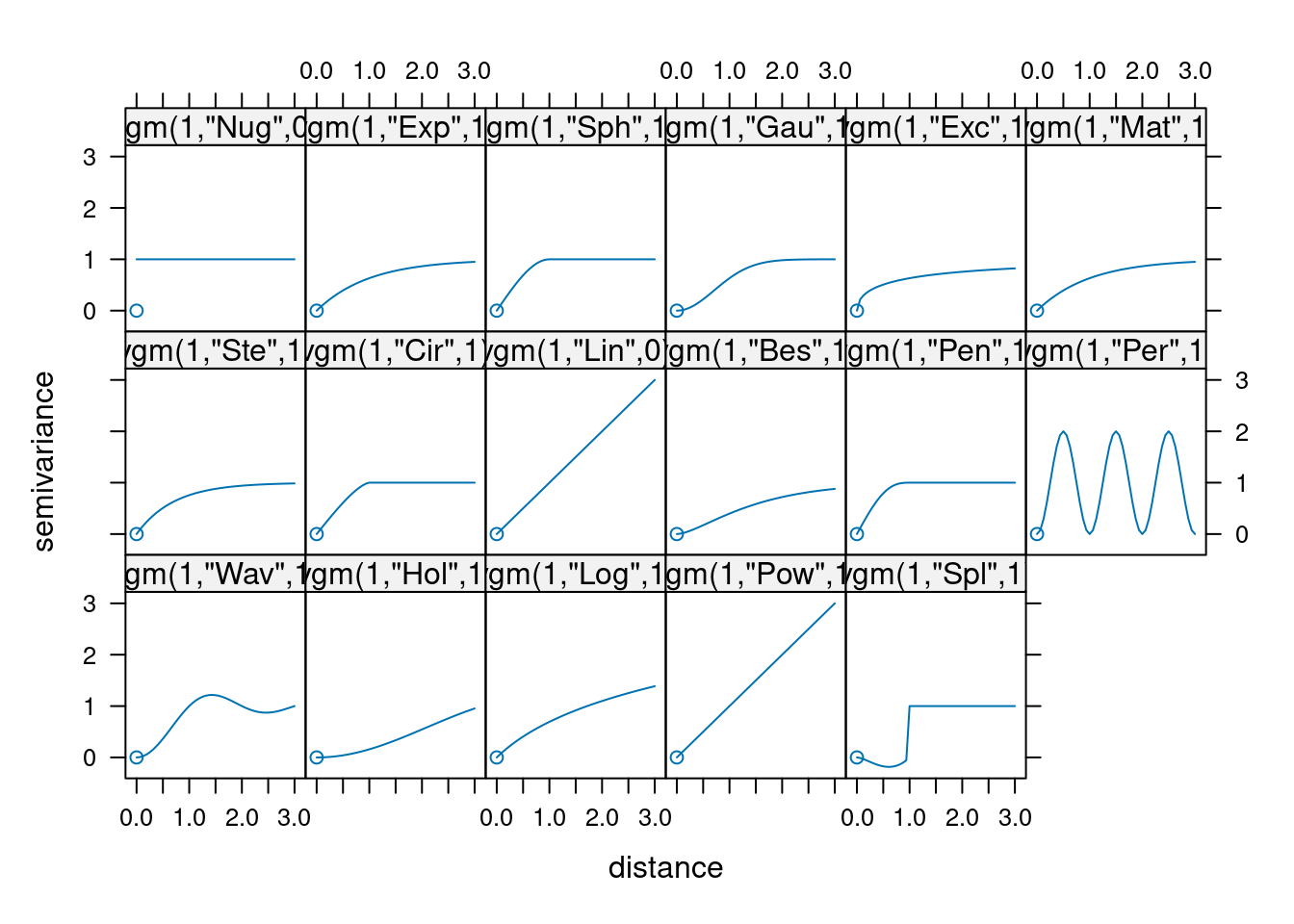

(vgm())

   short                                      long
1    Nug                              Nug (nugget)
2    Exp                         Exp (exponential)
3    Sph                           Sph (spherical)
4    Gau                            Gau (gaussian)
5    Exc        Exclass (Exponential class/stable)
6    Mat                              Mat (Matern)
7    Ste Mat (Matern, M. Stein's parameterization)
8    Cir                            Cir (circular)
9    Lin                              Lin (linear)
10   Bes                              Bes (bessel)
11   Pen                      Pen (pentaspherical)
12   Per                            Per (periodic)
13   Wav                                Wav (wave)
14   Hol                                Hol (hole)
15   Log                         Log (logarithmic)
16   Pow                               Pow (power)
17   Spl                              Spl (spline)
18   Leg                            Leg (Legendre)
19   Err                   Err (Measurement error)
20   Int                           Int (Intercept)

Un variogramme théorique est un objet de type vgm, qui doit être initialisé avec des paramètres avant de l’insérer dans la fonction d’estimation.

Un inconvénient dans la création d’un objet vgm est l’absence de nom pour certains paramètres, il faut se référer à la documentation pour savoir à quel place il faut rentrer quel argument lorsque’on appelle vgm(). Ne pas renseigner un argument initialise celui-ci à NA. Utiliser fit.variogram sur un objet avec des NA fait appel à une étape supplémentaire qui initialise avec des paramètres issus du variogramme empirique. Cela empêche de contrôler les valeurs initiales de l’estimation.

Estimation du variogramme théorique

Les paramètres du variogramme théorique sont ajustés par moindres carrés sur le variogramme empirique.

vgmModelwav <- fit.variogram(test,vgm(‘Wav’))

vgmModelexp <- fit.variogram(test, vgm(2, "Exp", 1000))
vgmModelexp

  model     psill    range
1   Exp 0.6849652 421.2255

vgmModelmat <- fit.variogram(test, vgm(10, "Mat", 300, 4.5, kappa = 0.7))
vgmModelmat

  model      psill    range kappa
1   Nug 0.05112814   0.0000   0.0
2   Mat 0.62395526 340.0403   0.7

vgmModelNA <- fit.variogram(test,vgm('Mat'))
vgmModelNA

  model       psill    range kappa
1   Nug 0.001864289   0.0000   0.0
2   Mat 0.684275121 424.4234   0.5

start_time <- Sys.time()
vgmModelwav <- fit.variogram(test,vgm('Wav'))
end_time <- Sys.time()
end_time - start_time

Time difference of 0.004230022 secs

vgmModelwav

  model     psill    range
1   Nug 0.1556503   0.0000
2   Wav 0.4407740 643.9395

La fonction plot() appelée sur un modèle estimé trace en continu le variogramme théorique et en points le variogramme empirique.

plot(test, vgmModelmat)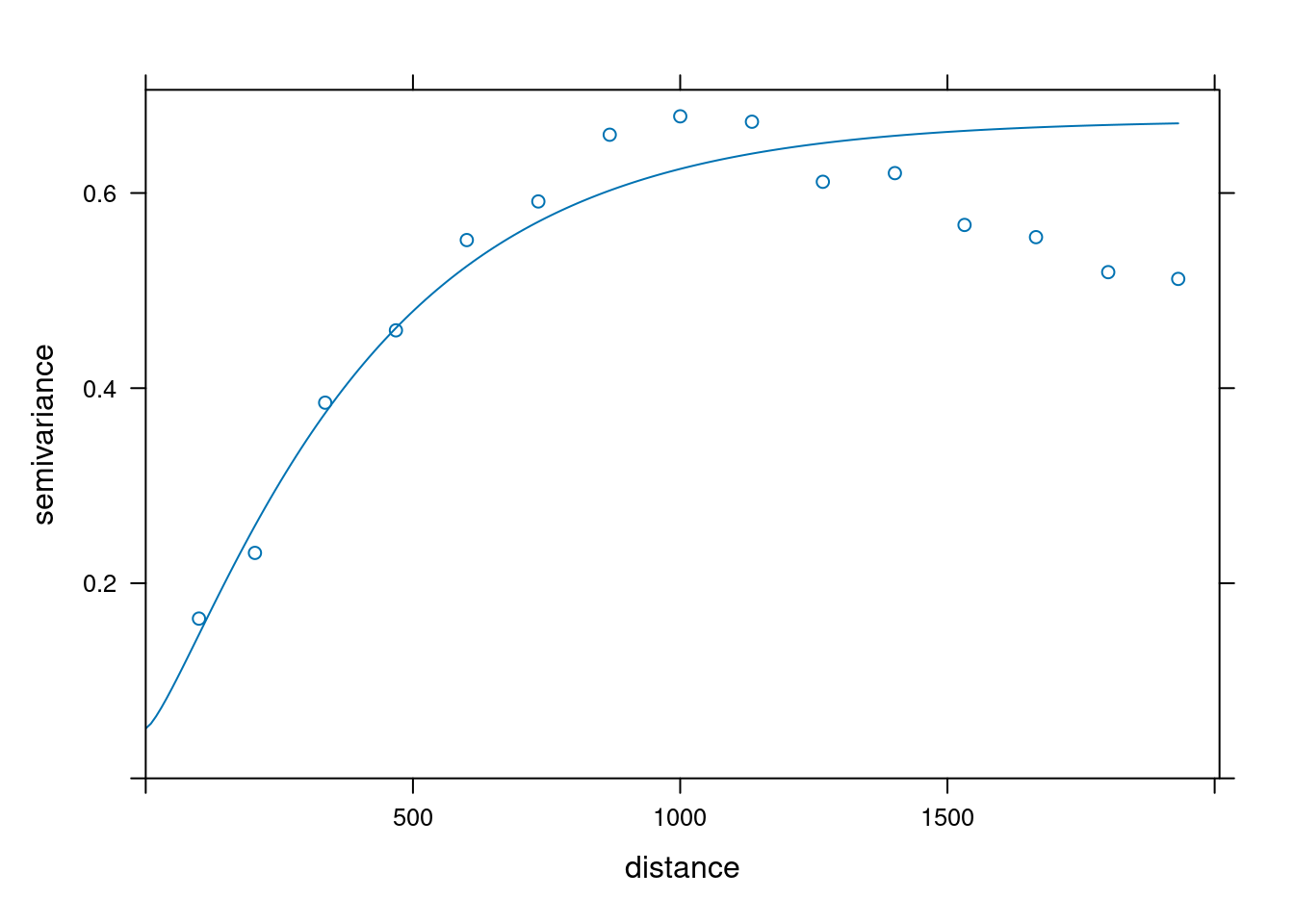

plot(test, vgmModelwav)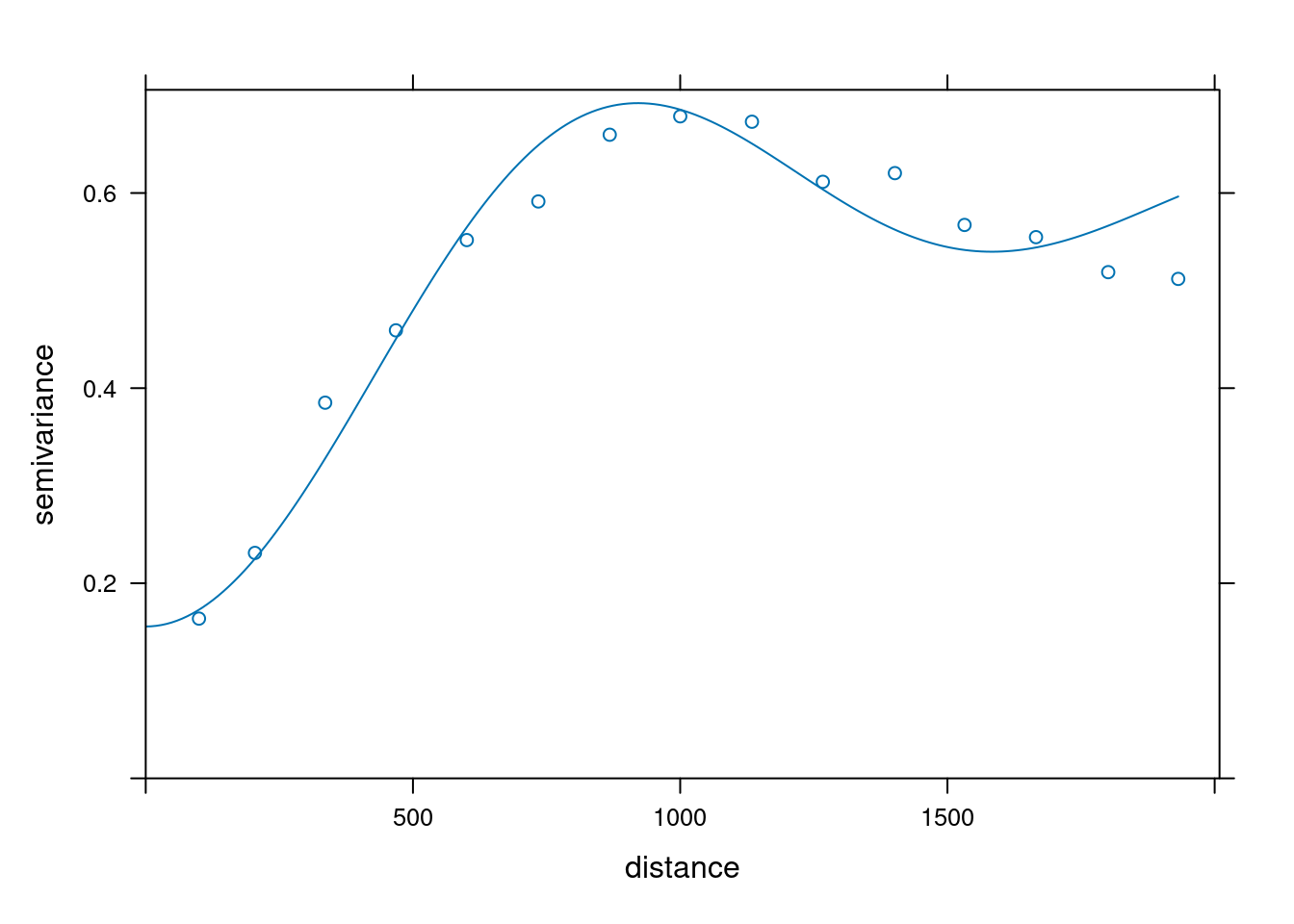

Krigeage

start_time <- Sys.time()
krig <- krige(log(zinc)~1 , df_sf, df_grid_sf, model = vgmModelmat)

[using ordinary kriging]

end_time <- Sys.time()
end_time - start_time

Time difference of 0.5332577 secs

Kres_pred = data.frame(x=meuse.grid$x,y=meuse.grid$y,pred=krig$var1.pred)
krig_res<- terra::rast(Kres_pred, type="xyz", crs="EPSG:2154")


Kres_var = data.frame(x=meuse.grid$x,y=meuse.grid$y,pred=krig$var1.var)
krig_var<- terra::rast(Kres_var, type="xyz", crs="EPSG:2154")

plot((krig_res), main = 'Krigeage de log(zinc) - gstat')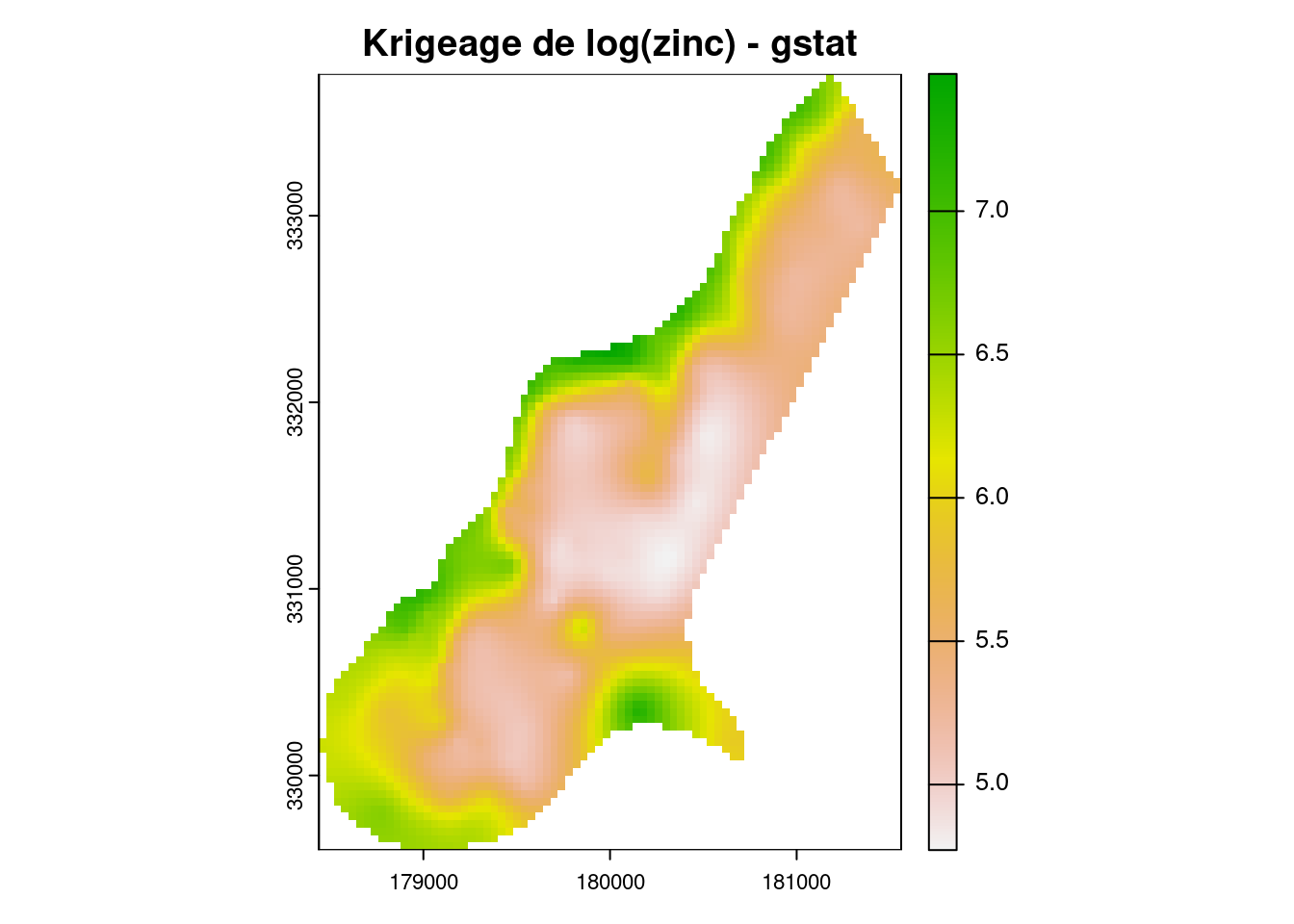

plot(krig_var,main = 'Erreur de krigeage pour log(zinc) - gstat')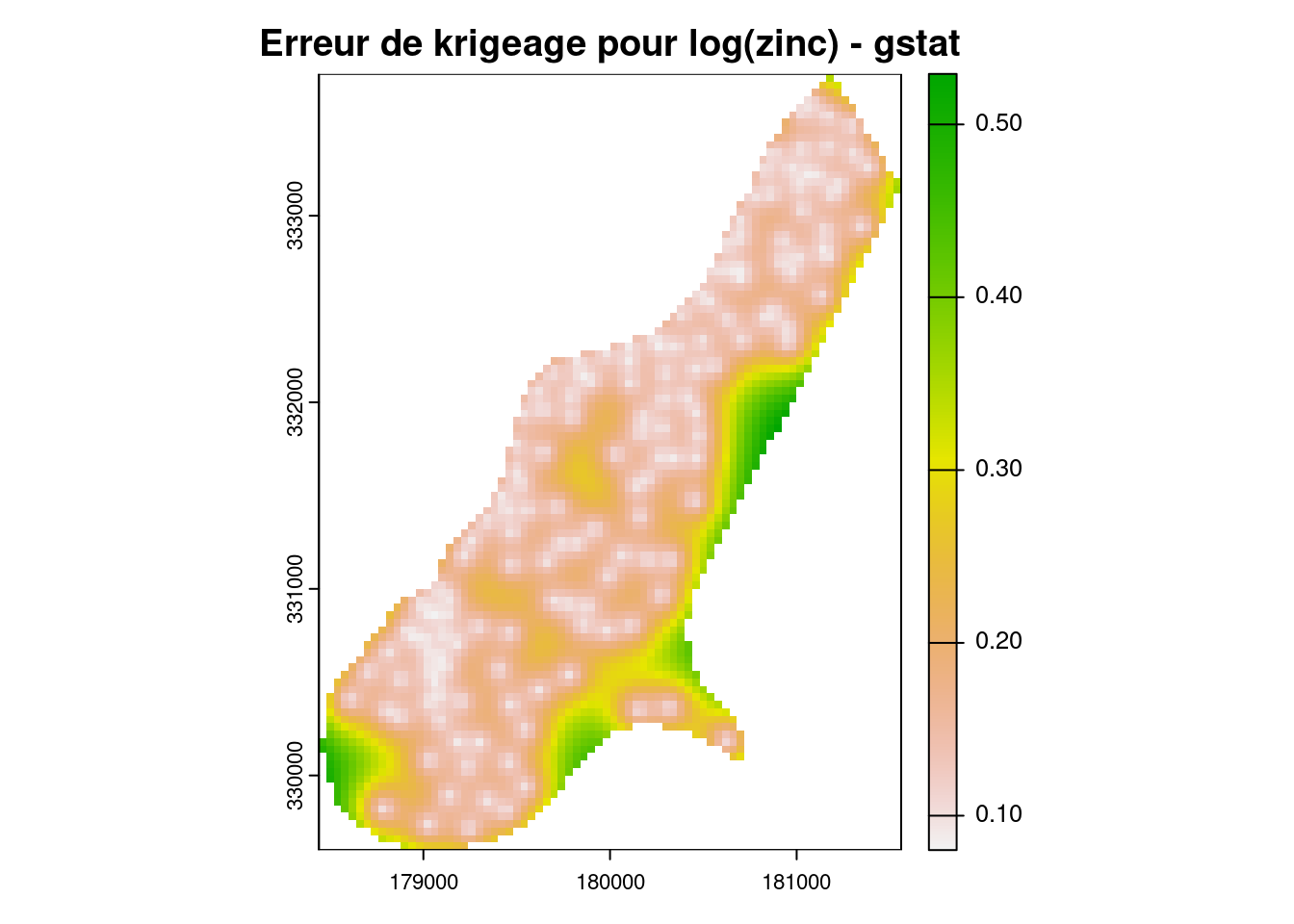

2 - Package R GeoModels

GeoModels est un package relativement récent (2022), il prend la suite de CompRandFld suite à une mise à jour majeure de R.

Il est disponible sur le CRAN :

https://CRAN.R-project.org/package=GeoModels

Le package propose des fonctions pour de la simulation, de l’inférence et de la prédiction de champs spatiaux et spatio-temporels, univarié ou multivarié. Il contient des méthode spour des champs Gaussiens et non Gaussiens.

On peut travailler en coordonnées euclidiennes et sphériques.

GeoModels propose de faire des modèles spatiaux et spatiotemporels.

Les estimations se font par maximisation de vraisemblance composite.

Du fait de la variété de modèles et de données possibles en entrée (spatial, spatiotemporel, 1 ou plusieurs variables …), chaque fonction est définie généralement pour prendre en entrée des données (notamment data et coordonnées) sous plusieurs types. Dans tous les cas, on ne dépend pas de structures “évoluées”, on n’a besoin que de vecteurs et de matrices. En contrepartie, on est probablement moins libres sur les systèmes de coordonnées.

Les données en entrée doivent être, si on fait du spatial uniquement :

- data : un vecteur de taille \(d\)

- coordx : une matrice \(d \times 2\) si on met directement les coordonnées, ou un vecteur de taille \(d\) si on sépare les coordonnées

- coordy : NULL si on a déjà mis les 2 coordonnées dans coordx, vecteur de taille \(d\) sinon.

Il n’y a donc pas besoin de gérer des types de données spatiales comme dans gstat.

data =log(df$zinc)

coordx = df$x

coordy = df$y

Variogramme empirique

# Variogramme empirique : 
start_time <- Sys.time()
emp_vario = GeoVariogram(data, coordx, coordy=coordy,numbins = 16,maxdist = 2000)

end_time <- Sys.time()
end_time - start_time

Time difference of 0.009788275 secs

plot(emp_vario,main = "Variogramme empirique Zinc - GeoModels")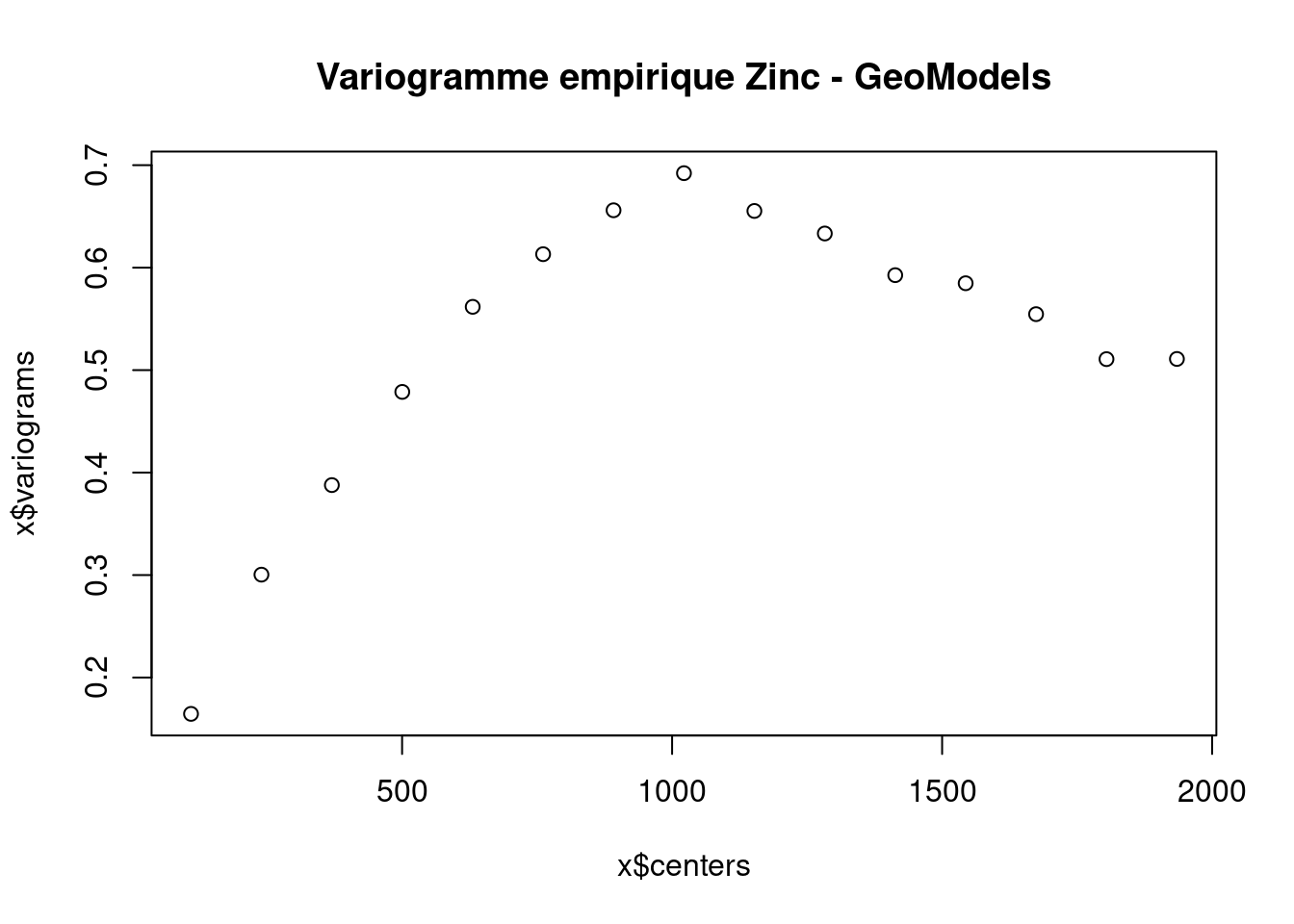

Modèles supportés

Voir documentation, fonction “GeoCovMatrix”

CorrParam, et NuisParam permettent d’obtenir la listes des paramètres requis pour les modèles.

NuisParam('Gaussian')

[1] "mean"   "nugget" "sill"  

CorrParam("Exp")

[1] "scale"

CorrParam('Matern')

[1] "scale"  "smooth"

Estimation du variogramme théorique

L’estimation nécessite de donner en entrée deux listes, fixed et start, correspondant aux paramètres fixés et libres dans l’ajustement.

ATTENTION : si on ne fixe rien, il ne faut pas une liste vide mais un NULL, ou alors ne pas renseigner l’argument (NULL est la valeur par défaut)

L’algorithme vérifiera automatiquement que tous les paramètres nécessaires sont remplis. Il n’y a pas comme dans gstat de méthode qui rempli automatiquement des oublis, il faut vérifier avec les fonctions précédentes qu’on a bien tout initialisé.

fixed = NULL

start = list( mean = 0 , sill=0.5,smooth=0.7,scale = 300,nugget = 0.044)

modelemat = GeoFit(data, coordx=coordx, coordy=coordy, fixed = fixed, start=start, 

corrmodel="Matern",distance="Eucl",maxdist = 2000)

modelemat

##################################################################
Maximum  Composite-Likelihood Fitting of Gaussian Random Fields

Setting: Marginal Composite-Likelihood 

Model: Gaussian 

Type of the likelihood objects: Pairwise 

Covariance model: Matern 

Optimizer: Nelder-Mead 

Number of spatial coordinates: 155 
Number of dependent temporal realisations: 1 
Type of the random field: univariate 
Number of estimated parameters: 5 

Type of convergence: Successful 
Maximum log-Composite-Likelihood value: -37443.52

Estimated parameters:
    mean    nugget     scale      sill    smooth  
  5.8692    0.9994  266.5697    0.5482   68.5193  

##################################################################

# Vario fit : il faut mettre en entrée des valeurs de départ et des valeurs qu'on fixe pour les paramètres

fixed = list(nugget = 0.044) #fixe la valeur obtenue avec gstat

start = list( mean = 0 , sill=0.5,smooth=0.7,scale = 300)

modelemat2 = GeoFit(data, coordx=coordx, coordy=coordy, fixed = fixed, start=start, 

corrmodel="Matern",distance="Eucl",maxdist = 2000)

modelemat2

##################################################################
Maximum  Composite-Likelihood Fitting of Gaussian Random Fields

Setting: Marginal Composite-Likelihood 

Model: Gaussian 

Type of the likelihood objects: Pairwise 

Covariance model: Matern 

Optimizer: Nelder-Mead 

Number of spatial coordinates: 155 
Number of dependent temporal realisations: 1 
Type of the random field: univariate 
Number of estimated parameters: 4 

Type of convergence: Successful 
Maximum log-Composite-Likelihood value: -37218.17

Estimated parameters:
    mean     scale      sill    smooth  
  5.8673  114.4160    0.5495    1.5971  

##################################################################

fixed = NULL

start = list( mean = 0 , sill=0.5,scale = 300,nugget = 0.044)

start_time <- Sys.time()
modelewav = GeoFit(data, coordx=coordx, coordy=coordy, fixed = fixed, start=start, 

corrmodel="Wave",distance="Eucl",maxdist = 2000)

end_time <- Sys.time()
end_time - start_time

Time difference of 0.755408 secs

modelewav

##################################################################
Maximum  Composite-Likelihood Fitting of Gaussian Random Fields

Setting: Marginal Composite-Likelihood 

Model: Gaussian 

Type of the likelihood objects: Pairwise 

Covariance model: Wave 

Optimizer: Nelder-Mead 

Number of spatial coordinates: 155 
Number of dependent temporal realisations: 1 
Type of the random field: univariate 
Number of estimated parameters: 4 

Type of convergence: Successful 
Maximum log-Composite-Likelihood value: -37191.31

Estimated parameters:
    mean    nugget     scale      sill  
  5.8669    0.3839  200.4165    0.5509  

##################################################################

On peut comparer les modèles que l’on vient de faire avec le variogramme empirique :

# Comparaison avec l'empirique matern :

GeoCovariogram(modelemat, distance="Eucl",show.vario= TRUE,vario = emp_vario)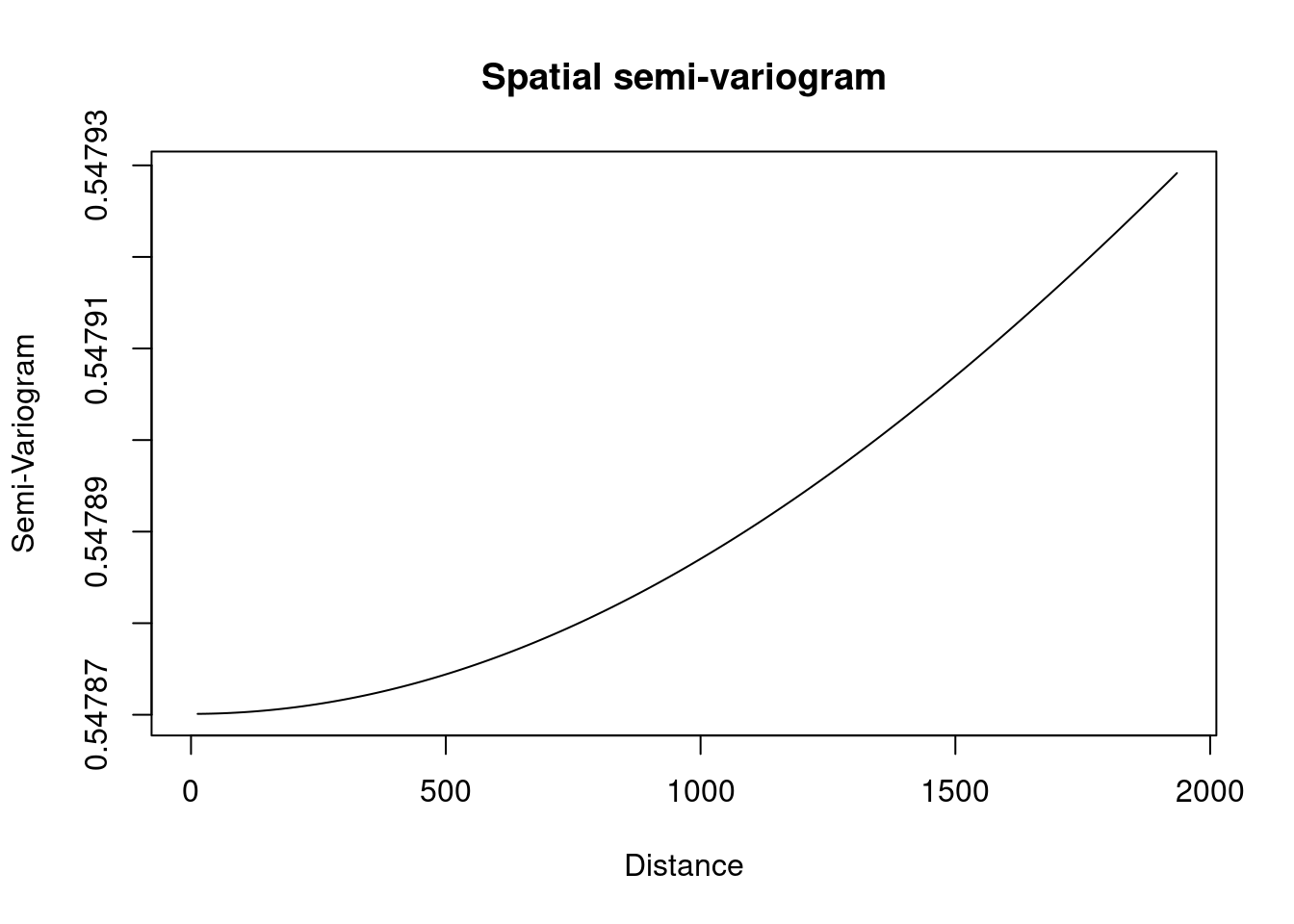

GeoCovariogram(modelemat2, distance="Eucl",show.vario= TRUE,vario = emp_vario)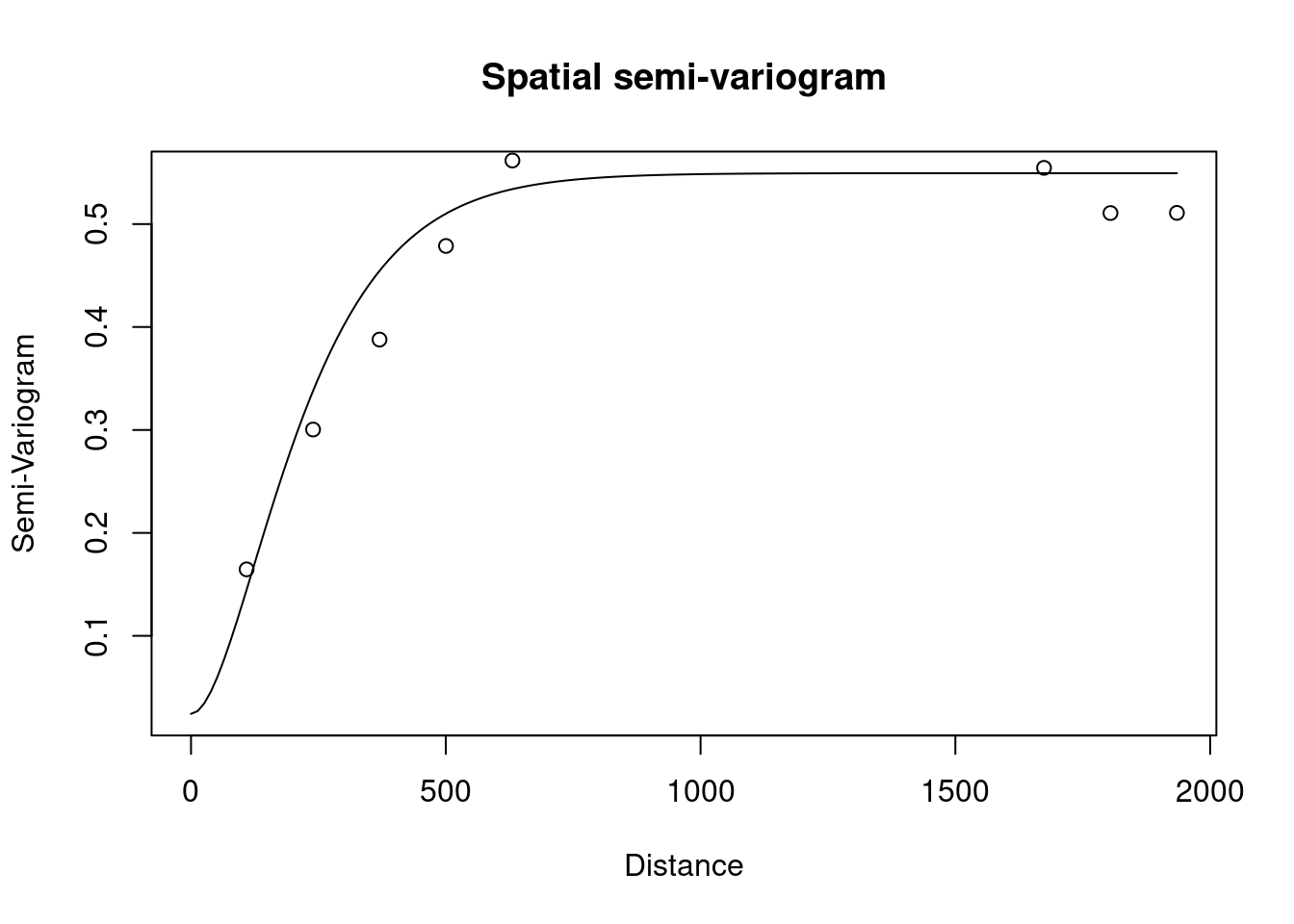

# Comparaison avec l'empirique Wave :

GeoCovariogram(modelewav, distance="Eucl",show.vario= TRUE,vario = emp_vario)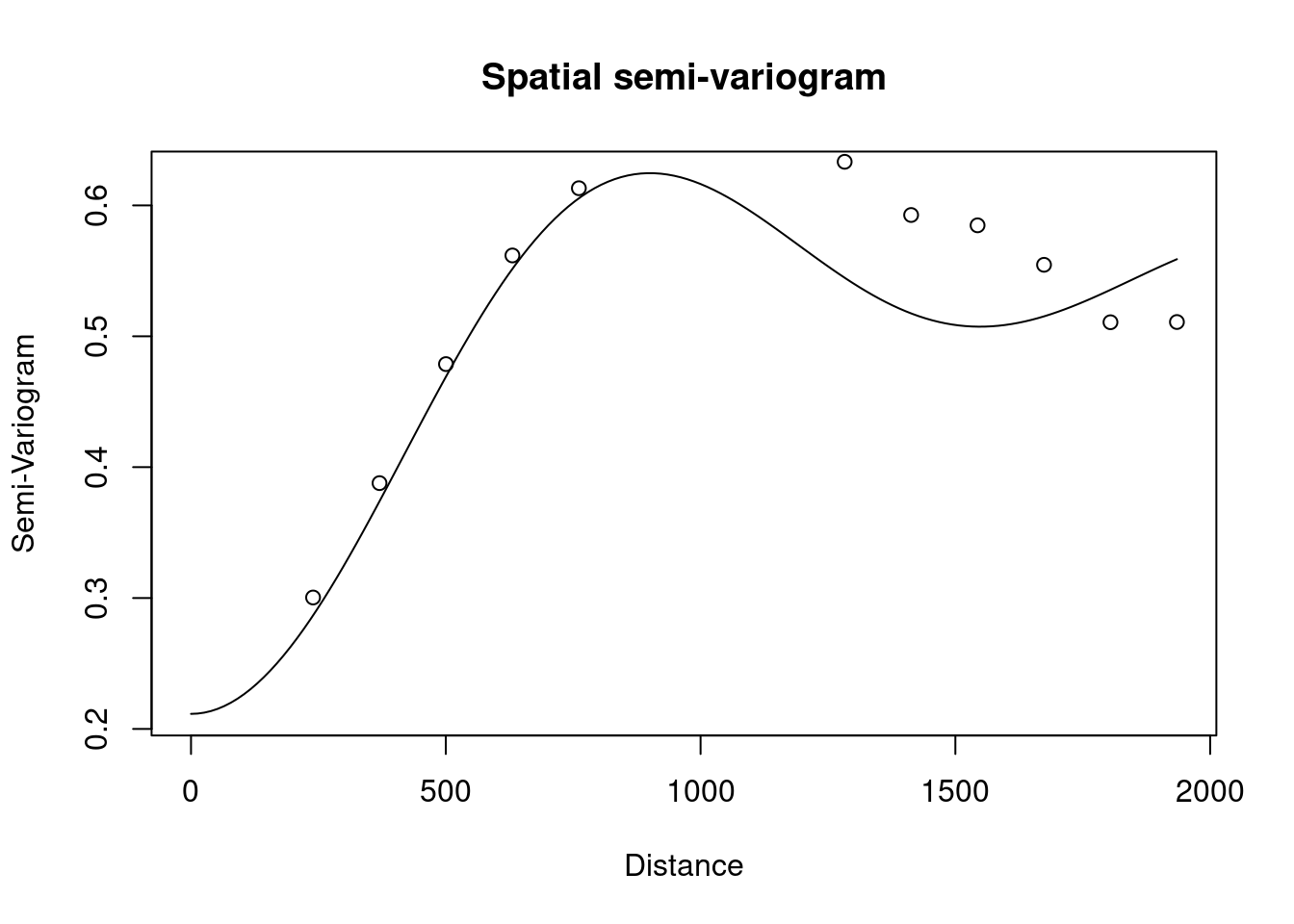

Krigeage

locskrig = data.frame (x =meuse.grid$x,y= meuse.grid$y)

start_time <- Sys.time()
krig_geomodels = GeoKrig(loc= locskrig,coordx=coordx, coordy=coordy,corrmodel = 'Wave',param = c(modelemat$fixed,modelewav$param),mse =TRUE,data=data)

end_time <- Sys.time()
end_time - start_time

Time difference of 0.7958126 secs

coords  = cbind(coordx,coordy)

Kres_pred_geo = data.frame(x=meuse.grid$x,y=meuse.grid$y,pred=krig_geomodels$pred)

krig_res_geo<- terra::rast(Kres_pred_geo, type="xyz", crs="EPSG:2154")

Kres_var_geo = data.frame(x=meuse.grid$x,y=meuse.grid$y,pred=krig_geomodels$mse)

krig_var_geo<- terra::rast(Kres_var_geo, type="xyz", crs="EPSG:2154")

plot((krig_res_geo), main = 'Krigeage de log(zinc) - GeoModels')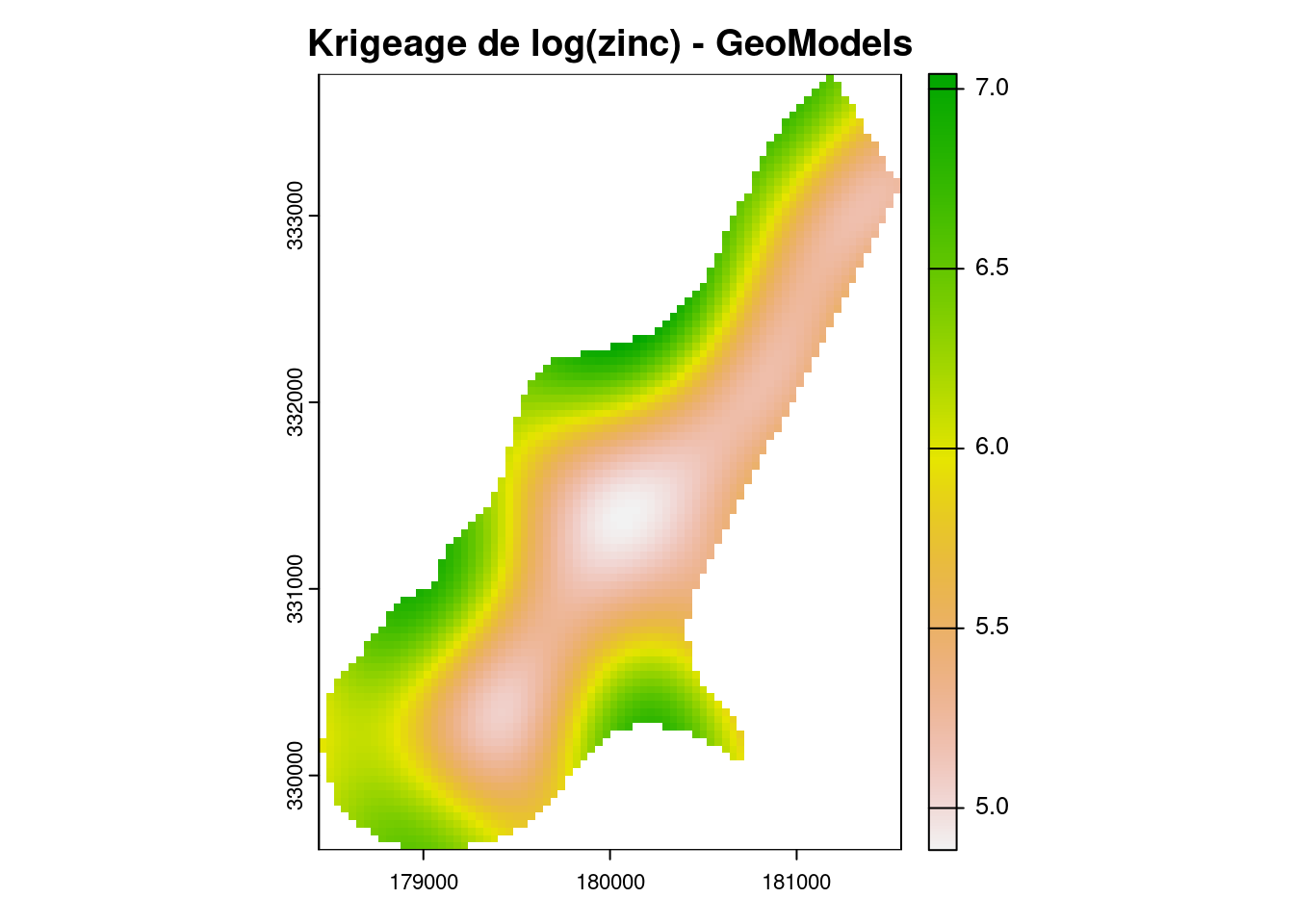

plot(krig_var_geo,main = 'Erreur de krigeage pour log(zinc) - GeoModels')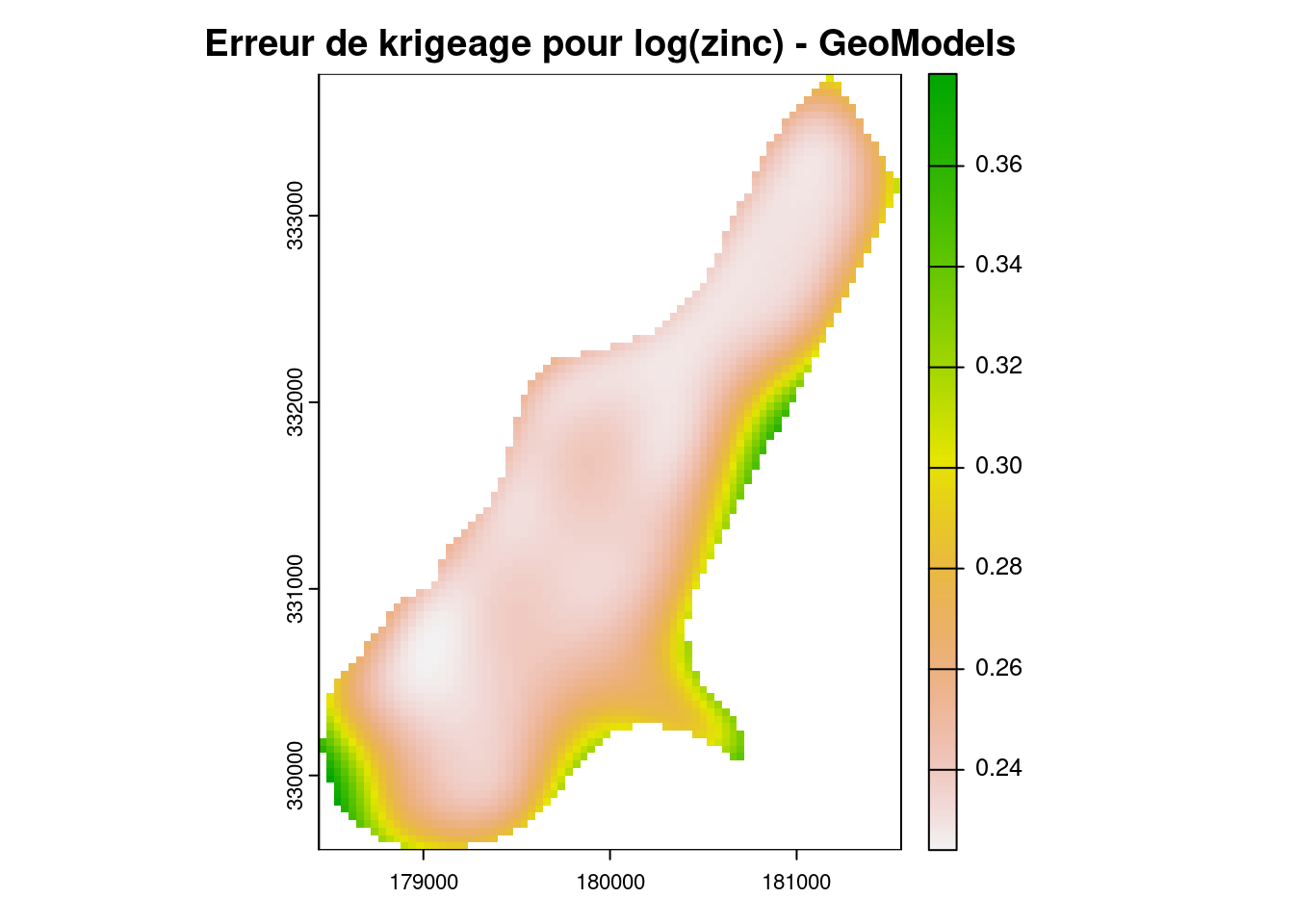

3 - Package Julia GeoStats

Julia est un langage de programmation de haut niveau, performant et dynamique pour le calcul scientifique, avec une syntaxe familière aux utilisateurs d’autres environnements de développement similaires (Matlab, R, Scilab, Python, etc.). Il fournit un compilateur sophistiqué, un système de types dynamiques avec polymorphisme paramétré, une exécution parallèle distribuée, des appels directs de fonctions C, Fortran et Python. (source Wikipedia)

Un avantage de Julia est la possibilité d’écrire en LaTeX dans les lignes de code.

GeoStats est un package récent (avril 2015), sa dernière mise à jour date de 3 mois, c’est le package majeur en statistiques spatiales de Julia.

Il est disponible sur le :

https://juliaearth.github.io/GeoStats.jl/stable/

Pour l’installer faire la commande suivante dans le terminal de votre IDE : ]add GeoStats

Le package propose des fonctions pour de la simulation, de l’inférence et de la prédiction de champs spatiaux

On peut travailler en coordonnées euclidiennes et sphériques.

GeoStats propose de faire des modèles spatiaux. Sa particularité va être de tester tous les variogrammes disponibles (dans une même exécution) dans le package pour obtenir le plus optimisé avec les paramètres qui fonctionnent le mieux.

Bibliothèques Julia

# Import package
using GeoDataFrames, Distributed, StatsAPI, Plots, DelimitedFiles, DataFrames, CSV, GeoStats, Rasters,  Shapefile,GeoTables, CairoMakie; const GDF=GeoDataFrames; import WGLMakie as Mke

Importer les données

# Get the current working directory
current_directory = pwd()

#import data
meuse = CSV.read(joinpath(current_directory,"meuse.txt"),DataFrame;delim="," )
meuse_grid = CSV.read(joinpath(current_directory, "meuse.grid.txt"),DataFrame; delim=",")
meuse_geom = georef(CSV.File(joinpath(current_directory,"meuse.txt")),(:x,:y,:cadmium))

#describe data
describe(meuse)
describe(meuse_grid)

Transformation en données spatiale

#add log zinc to the data
logmeuse = log.(meuse.zinc)
meuse.logzinc = logmeuse

#create coord of data meuse
coord = [(x, y) for (x, y) in zip(meuse.x, meuse.y)]
#create spatial object of meuse
meuselog = georef(meuse[:,["x","y","logzinc"]],coord)

# list of properties with coordinates
props = (logzinc=meuse.logzinc,)
𝒟 = georef(props, coord)

Variogramme

Le fit pour tester les différents variogramme va nous donner le SineHoleVariogram avec tous les paramètres optimisé. On décide à la base d’utiliser ce dernier mais il s’avère qu’il ne donne pas de bon résultat pour le Krigeage. On utilisera donc un variogramme de Matérn. Si vous voulez observer ce dernier dans le krigeage il suffira de mettre dans la fonction kriging, le variogramme désiré.

# empirical variogram

@time empvario = EmpiricalVariogram(meuselog, :logzinc, maxlag = 2000.)

## plot of empirical variogram
# Mke.plot(empvario) plot interactive
# CairoMakie.plot(empvario) #plot sans interaction
## plot theorical variogram
# CairoMakie.plot(MaternVariogram(range=691, nugget=0.04))
# CairoMakie.plot(SineHoleVariogram(range=691, nugget=0.25))

#fit theorical and empirical variogramand 
@time fitvario = fit(Variogram, empvario)

# CairoMakie.plot(empvario)
# CairoMakie.plot!(fitvario, maxlag = 2000.)
# CairoMakie.current_figure()

Création de la grille

# grid creation
# Convert the x and y coordinates to numeric arrays
x_coords = Float64.(meuse.x)
y_coords = Float64.(meuse.y)# Create the Cartesian grid dimensions, origin, and spacing
dims = (100, 100)  # Number of grid points in x and y directions
origin = (minimum(x_coords), minimum(y_coords)) # Lower left corner of the grid
spacing = ((maximum(x_coords) - minimum(x_coords)) / (dims[1] - 1),
           (maximum(y_coords) - minimum(y_coords)) / (dims[2] - 1)) 
 # Cell spacing in x and y directions# Create the CartesianGrid
𝒢 = CartesianGrid(dims, origin, spacing)

Krigeage

𝒫 = EstimationProblem(𝒟, 𝒢, :logzinc)

@time 𝒮 = Kriging(:logzinc => (variogram=MaternVariogram(nugget = 0.21,sill = 0.59,range=706.78),))

# perform estimation
@time Ω = solve(𝒫, 𝒮)

# CairoMakie.plot(Ω.geometry, color = Ω.logzinc_variance)

Affichage du Krigeage

#Export Kriging
GeoTables.save(joinpath(current_directory,"data_geostats_julia/Kriging2.shp"), Ω,force=true )

#read kriging
shape =  Shapefile.Handle(joinpath(current_directory,"data_geostats_julia/Kriging2.shp")).shapes
# read grid 
grid_shp =  Shapefile.Handle(joinpath(current_directory,"data_geostats_julia/boundary1.shp")).shapes

# Define a reducer function (e.g., to sum values within each cell)
reducer(cell_values) = sum(cell_values)

rasterized_krig = rasterize(shape, fill=Ω.logzinc, reducer = reducer, size=(100, 100))
Plots.plot(rasterized_krig)

Burning each geometry to a BitArray slice...   0%|                                                  |  ETA: 0:48:28

Burning each geometry to a BitArray slice... 100%|██████████████████████████████████████████████████| Time: 0:00:00

Reducing...   4%|██                                                |  ETA: 0:00:02

Reducing...  47%|███████████████████████▌                          |  ETA: 0:00:00

Reducing...  89%|████████████████████████████████████████████▌     |  ETA: 0:00:00

Reducing... 100%|██████████████████████████████████████████████████| Time: 0:00:00

#Crop 
masked = mask(rasterized_krig,with=grid_shp)
Plots.plot(masked, title = "Krigeage logzinc")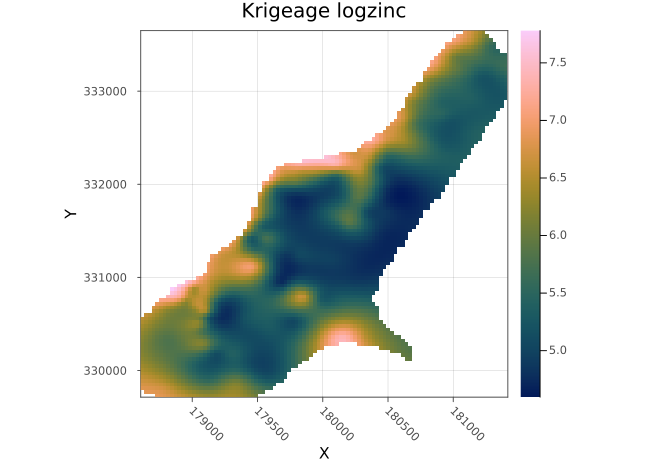

4 - Comparaison

Package	R : gstat	R : GeoModels	Julia : GeoStats
Type de données d’entrée	sp, sf	matrices, vecteurs	dataframes Coordonées de type CartesianGrid Inconvénient : peu de documentation - difficile à prendre en main
Documentation	CRAN	CRAN https://vmoprojs.github.io/GeoModels-page/	https://github.com/JuliaEarth/GeoStats.jl https://juliapackages.com/p/geostats
Estimation de paramètres du variogramme	Moindres carrés sur variogramme empirique 1 modèle à la fois au choix	Vraisemblance composite sur les données 1 modèle à la fois Paramètres fixes ou variables au choix	Moindres carrés sur le variogramme empirique Tous les modèles disponibles à la fois
Vitesse d’exécution - estimation du variogramme empirique	0.05s	0.07s	0.012s
Vitesse d’exécution - estimation du variogramme théorique	0.04s	1.15s	0.05s (TOUS LES MODELES)
Vitesse d’exécution - krigeage	0.42s	0.87s	0.08s (Kriging) 10.6s (solve)