VAE

library(tidyverse)
library(torch)

Ce document illustre un essai d’auto-encodeur variationnel utilisant la librairie torch.

Example simple (données mutivariées, sans structures)

Simulation de données

On commence par simuler des données suivant des gaussiennes pseudo-dégénérées, via une matrice $R$ de taille $15 \times 2$

\[ \begin{align*} Z & \sim \mathcal{N}_2(0, I_2) \\ Y = \mu + RZ + E & \sim \mathcal{N}_{15}(0, RR^T + \sigma^2 I_{15}) \end{align*} \]

Pour créer une structure de groupe naturelle, on simule 2 groupes de données, chacun avec son propre $\mu$ et son propre $R$

set.seed(42)
n <- 200
k <- 2
p <- 15
sigma <- 0.1
A <- matrix(rnorm(p*k), nrow = p, ncol = k)
B <- matrix(rnorm(p*k), nrow = p, ncol = k)
Y_A <- matrix(rnorm(n*k), nrow = n, ncol = k)  %*% t(A) + sigma * matrix(rnorm(n*p), nrow = n, ncol = p)
mean_A <- rep(1, n) %o% rnorm(p)
Y_B <- matrix(rnorm(n*k), nrow = n, ncol = k)  %*% t(B) + sigma * matrix(rnorm(n*p), nrow = n, ncol = p)
mean_B <- rep(1,n) %o% rnorm(p)
input <- torch_tensor(rbind(Y_A + mean_A, Y_B + mean_B))

On va construire un auto-encoder avec un espace latent de dimension latent_dim égale à 2 pour pouvoir faire des dessins.

latent_dim <- 2

Définition d’un encodeur

On définit ensuite un encodeur comme un réseau très simple avec deux couches linéaires de tailles 10 puis 5 et des fonctions d’activation relu (hormis pour la couche finale de répresentation).

La construction passe par la définition d’un module (via nn_module()) auquel il faut (au moins) fournir 2 méthodes:

initialize() qui indique comment initialiser une nouvelle instance du réseau (et définit l’architecture du réseau)
forward() qui indique comment réaliser les calculs

encoder <- nn_module(
  classname = "encoder", 
  ## Définition des couches
  initialize = function(in_features, latent_dim) {
    self$linear1 <- nn_linear(in_features, 10)
    self$linear2 <- nn_linear(10, 5)
    self$mean <- nn_linear(5, latent_dim)
    self$log_var  <- nn_linear(5, latent_dim)
  }, 
  ## Définitions des calculs
  forward = function(input) {
    ## Combinaison linéaire des features dans la première couche
    input <- self$linear1(input)
    ## Activation relu
    input <- nnf_relu(input)
    ## Combinaison linéaire des features dans la deuxième couche
    input <- self$linear2(input)
    ## Activation relu
    input <- nnf_relu(input)
    ## Création des paramètres de moyenne et de variance
    mean <- self$mean(input)
    log_var   <- self$log_var(input)
    ## L'encodeur renvoie mean et sd
    list(mean    = mean, 
         log_var = log_var)
  }
)

On peut aussi définir ce module de façon plus compacte en utilisant nn_sequential() pour chaîner des module et indiquer dans la définition les fonctions d’activation à utiliser.

## Création d'un module compressor
create_compressor <- function(in_features) {
  nn_sequential(
    nn_linear(in_features, 10),
    nn_relu(),
    nn_linear(10, 5),
    nn_relu()
  )  
}
## Création de l'encodeur à l'aide du compresseur
encoder <- nn_module(
  classname = "encoder", 
  ## Définition des couches
  initialize = function(in_features, latent_dim) {
    self$compressor <- create_compressor(in_features)
    self$mean <- nn_linear(5, latent_dim)
    self$log_var  <- nn_linear(5, latent_dim)
  }, 
  ## Définitions des calculs
  forward = function(input) {
    ## Calcul des répresentations compressées
    compressed <- self$compressor(input)
    ## Création des paramètres de moyenne et de variance
    mean <- self$mean(compressed)
    log_var   <- self$log_var(compressed)
    ## L'encodeur renvoie mean et log_var
    list(mean    = mean, 
         log_var = log_var)
  }
)

L’encodeur produit deux vecteurs de taille latent_dim à partir d’un vecteur de données (de taille 15).

On peut le vérifier sur un exemple simple

enc <- encoder(15, 2)
enc(input[1:5, ])

## $mean
## torch_tensor
## -0.2367  0.2638
## -0.2978  0.2221
## -0.3095  0.2072
## -0.2217  0.2028
## -0.1933  0.2651
## [ CPUFloatType{5,2} ][ grad_fn = <AddmmBackward0> ]
## 
## $log_var
## torch_tensor
## -0.2825  0.2240
## -0.2865  0.2351
## -0.2588  0.2478
## -0.5191  0.5796
## -0.1657  0.3050
## [ CPUFloatType{5,2} ][ grad_fn = <AddmmBackward0> ]

Définition d’un décodeur

On crée ensuite notre décodeur de la même façon. Ce dernier va partir d’un vecteur de taille latent_dim pour construire un vecteur de taille 15. Par souci de simplicité, on adopte une architecture symétrique à celle du décodeur à l’exception de la dernière couche (purement linéaire).

## Création d'un module decompressor
create_decompressor <- function(latent_dim, out_features) {
  nn_sequential(
    nn_linear(latent_dim, 5),
    nn_relu(),
    nn_linear(5, 10),
    nn_relu(),
    nn_linear(10, out_features),
  )  
}
## Création du decodeur à l'aide du decompresseur
decoder <- nn_module(
  classname = "decoder", 
  ## Définition des couches
  initialize = function(latent_dim, out_features) {
    self$decompressor <- create_decompressor(latent_dim, out_features)
  }, 
  ## Définitions des calculs
  forward = function(input) {
    self$decompressor(input)
  }
)

Le décodeur produit un vecteur de taille out_features à partir d’un vecteur de taille latent_dim. On peut le vérifier sur un exemple simple.

dec <- decoder(2, 15)
latent_vectors <- matrix(0, nrow = 5, ncol = 2) |> torch_tensor() 
dec(latent_vectors)

## torch_tensor
## Columns 1 to 10-0.1807  0.1197 -0.4323  0.2239  0.0253 -0.3600  0.2588 -0.2101 -0.0428  0.0139
## -0.1807  0.1197 -0.4323  0.2239  0.0253 -0.3600  0.2588 -0.2101 -0.0428  0.0139
## -0.1807  0.1197 -0.4323  0.2239  0.0253 -0.3600  0.2588 -0.2101 -0.0428  0.0139
## -0.1807  0.1197 -0.4323  0.2239  0.0253 -0.3600  0.2588 -0.2101 -0.0428  0.0139
## -0.1807  0.1197 -0.4323  0.2239  0.0253 -0.3600  0.2588 -0.2101 -0.0428  0.0139
## 
## Columns 11 to 15-0.0240 -0.2368 -0.1406  0.0034 -0.1010
## -0.0240 -0.2368 -0.1406  0.0034 -0.1010
## -0.0240 -0.2368 -0.1406  0.0034 -0.1010
## -0.0240 -0.2368 -0.1406  0.0034 -0.1010
## -0.0240 -0.2368 -0.1406  0.0034 -0.1010
## [ CPUFloatType{5,15} ][ grad_fn = <AddmmBackward0> ]

Définition du VAE

La dernière étape consiste à coupler l’encodeur et le décodeur via un échantillonneur:

vae_module <- nn_module(
  classname = "sampler", 
  initialize = function(n_features, latent_dim) {
    self$latent_dim <- latent_dim
    self$encoder <- encoder(n_features, latent_dim)
    self$decoder <- decoder(latent_dim, n_features)
  },
  forward = function(input) {
    ## compression des données
    comp_input <- self$encoder(input)
    mean <- comp_input$mean
    log_var <- comp_input$log_var
    ## échantillonnage dans l'espace latent
    z <- mean + torch_exp(log_var$mul(0.5))*torch_randn(c(dim(input)[1], self$latent_dim))
    ## décompression de la représentation latente
    decomp_input <- self$decoder(z)
    
    list(decomp_input = decomp_input, 
         z            = z, 
         mean         = mean, 
         log_var      = log_var)
  }
)

Pour chaque vecteur de taille n_features, notre vae produit:

3 vecteurs de taille latent_dim (dont un aléatoire)
1 vecteurs de taille n_features

vae <- vae_module(n_features = 15, latent_dim = 2)
vae(input[1, , drop = FALSE])

## $decomp_input
## torch_tensor
## Columns 1 to 10-0.1937 -0.2174  0.0211 -0.1133  0.2024 -0.2526  0.1965  0.1724 -0.2878 -0.0811
## 
## Columns 11 to 15-0.0842 -0.2113  0.0400 -0.3169 -0.5942
## [ CPUFloatType{1,15} ][ grad_fn = <AddmmBackward0> ]
## 
## $z
## torch_tensor
## -1.4419 -0.0937
## [ CPUFloatType{1,2} ][ grad_fn = <AddBackward0> ]
## 
## $mean
## torch_tensor
## -0.2533  0.1497
## [ CPUFloatType{1,2} ][ grad_fn = <AddmmBackward0> ]
## 
## $log_var
## torch_tensor
##  0.4164  0.1739
## [ CPUFloatType{1,2} ][ grad_fn = <AddmmBackward0> ]

On peut vérifier que le composant z est aléatoire en appelant vae() deux fois.

## Premier appel
vae(input[1, , drop = FALSE])$z

## torch_tensor
## -2.6071 -0.0753
## [ CPUFloatType{1,2} ][ grad_fn = <AddBackward0> ]

## Deuxième appel
vae(input[1, , drop = FALSE])$z

## torch_tensor
## -1.5908 -0.2772
## [ CPUFloatType{1,2} ][ grad_fn = <AddBackward0> ]

Création du VAE et de l’optimiseur

On (ré-)initialise notre VAE

vae <- vae_module(n_features = 15, latent_dim = 2)

Et on prépare un optimiseur

optimizer_vae <- optim_adam(vae$parameters, lr = 0.001)

Entraînement du VAE

Dans cette partie, on se contente de charger l’ensemble des données, on ne travaille par batch (ce qui nécessiterait de définir un dataloader()).

On commence par définir une fonction de perte comme la somme de l’entropie croisée et de la divergence de Kullback-Leibler

loss_fn <- function(prediction, target, mean, log_var) {
  ## Perte L2 pour la reconstruction 
  cross_entropy <- nn_mse_loss(reduction = "sum")
  
  ## KL part of the loss
  kl <- function(mean, log_var) {
    kl_div <- 1 + log_var - mean$square() - log_var$exp()
    kl_div$multiply(-0.5)$sum()
  }
  
  ## Addition des deux 
  cross_entropy(prediction, target) + kl(mean, log_var)  
}
eval_loss <- function(input) {
  target <- input
  
  ## Extraction des composant prediction, mean, log_var depuis le VAE
  results <- vae(input)
  mean <- results$mean
  log_var <- results$log_var
  prediction <- results$decomp_input
  
  loss_fn(prediction, target, mean, log_var)
}

On vérifie sur un exemple simple que la fonction de perte est bien définie et vaut ce qu’on pense sur des exemples simples.

loss_fn(prediction = input[1, , drop = FALSE], 
        target = input[1, , drop = FALSE], 
        mean = torch_zeros(2),
        log_var = torch_zeros(2))

## torch_tensor
## 0
## [ CPUFloatType{} ]

Puis on entraîne notre modèle (comme vu dans l’atelier sur torch) pendant 1000 itérations.

num_iterations <- 1000
loss_vector <- vector("numeric", num_iterations)
for (i in 1:num_iterations) {
  optimizer_vae$zero_grad()
  loss <- eval_loss(input)
  loss$backward()
  loss_vector[i] <- loss |> as.numeric()
  optimizer_vae$step()
}

On peut regarder l’évolution de la perte au fil du temps.

plot(1:num_iterations, loss_vector)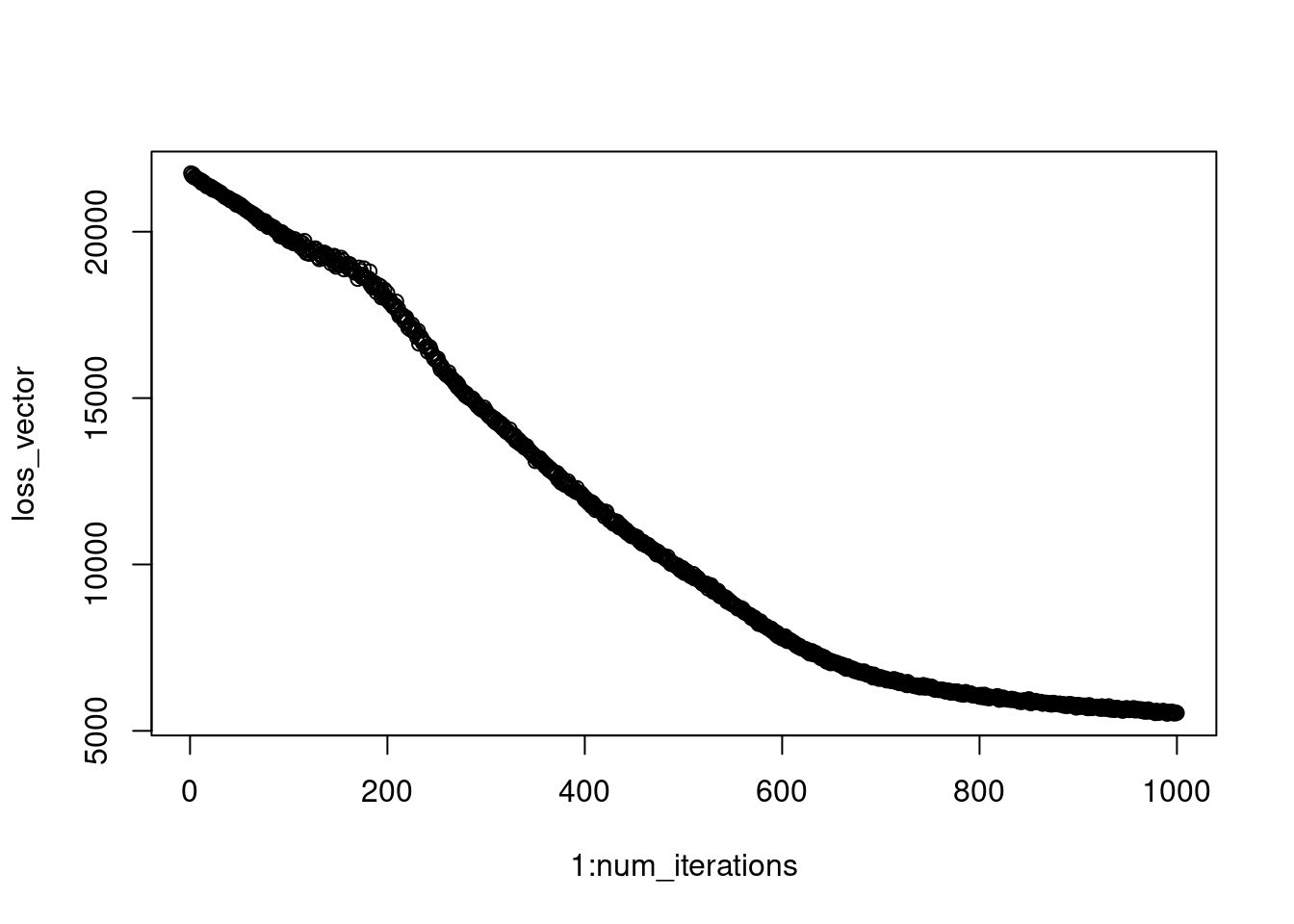

Exploration des résultats

On peut visualiser la représentation des données dans notre espace latent. On peut se contenter de faire tourner l’encodeur pour ça.

latents <- vae$encoder(input)$mean

Et les afficher

latents |> as.matrix() |> `colnames<-`(c("x", "y")) |> as_tibble() |> 
  mutate(group = rep(c("A", "B"), each = n)) |> 
  ggplot() + aes(x, y, color = group) + 
  geom_point() + 
  coord_equal() + 
  theme_minimal() + 
  theme(text = element_text(size = 16))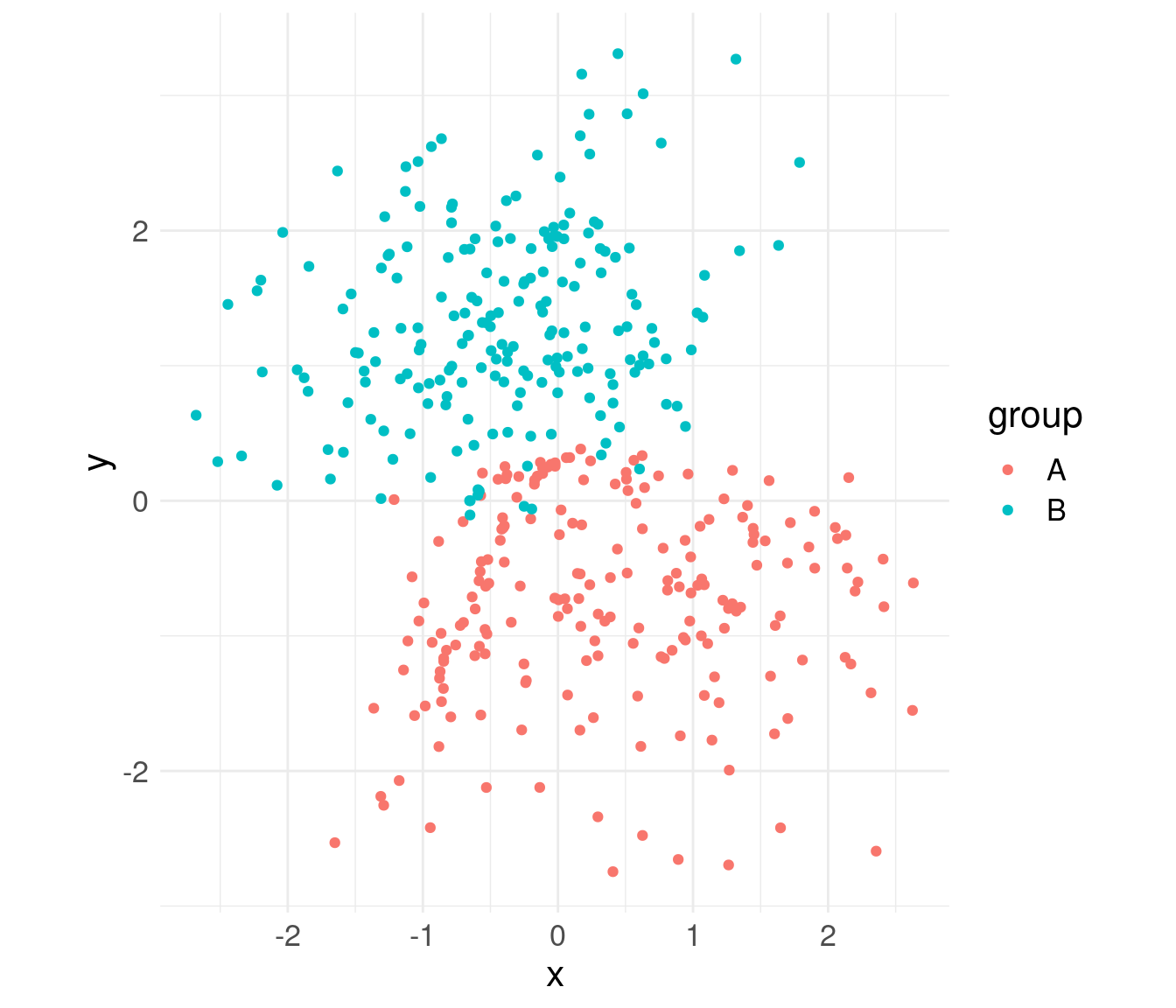

On peut aussi vérifier comment se positionne les reconstructions par rapport aux données originales (après avoir fait une ACP sur le tableau complet).

reconstructions <- vae(input)$decomp_input |> 
  as.matrix() %>% `colnames<-`(paste0("D", 1:ncol(.)))
pca <- prcomp(rbind(input |> as.matrix(), reconstructions), scale. = TRUE, center = TRUE)
point_data <- pca$x %>% 
  as_tibble() %>% 
  mutate(origin = rep(c("true", "fake"), each = nrow(input)), 
         group = rep(c("A", "B", "A", "B"), each = n))
line_data <- point_data |> mutate(ID = rep(1:nrow(input), 2)) |> 
  pivot_wider(id_cols = c(ID, group), names_from = origin, values_from = starts_with("PC"))

ggplot() +
  geom_point(data = point_data, mapping = aes(x = PC1, y = PC2, color = origin, shape = group)) +
  # geom_segment(data = line_data, mapping = aes(x = PC1_true, xend = PC1_fake, y = PC2_true, yend = PC2_fake), color = "grey80") +
  coord_equal() +
  theme_minimal() +
  facet_wrap(~ group) +
  theme(text = element_text(size = 16))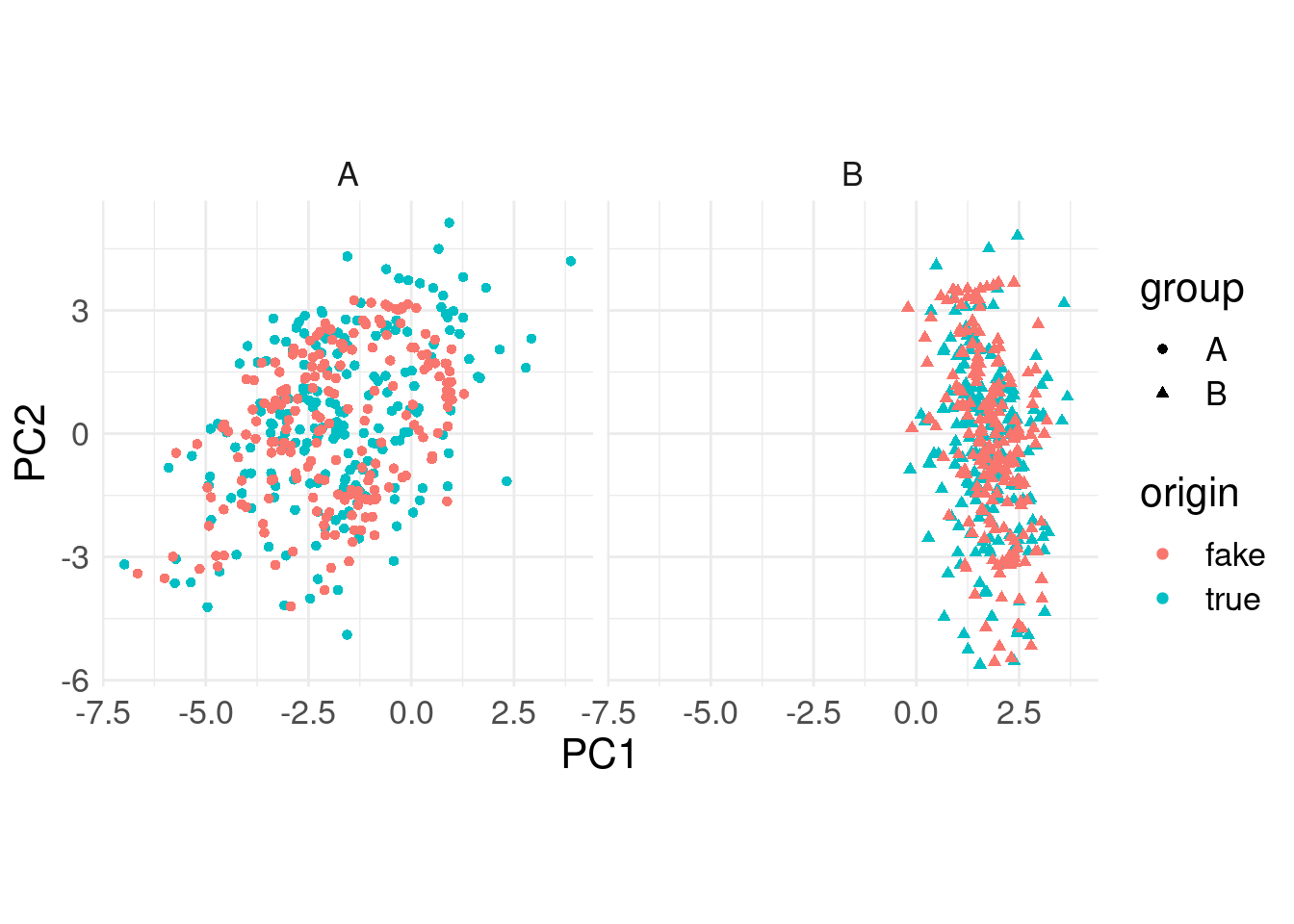

plot_data <- point_data |> mutate(ID = rep(1:nrow(input), 2)) |> 
  pivot_longer(cols = starts_with("PC"), names_to = "PC", values_to = "value") |> 
  pivot_wider(id_cols = c(ID, group, PC), names_from = "origin", values_from = "value") |> 
  filter(PC %in% paste0("PC", 1:4))

ggplot(plot_data, aes(x = true, y = fake, color = group)) + 
  geom_point() + 
  geom_abline(slope = 1, intercept = 0, color = "grey80") + 
  labs(x = "Original value", y = "Reconstructed value") + 
  facet_grid(group ~ PC) + 
  theme_minimal()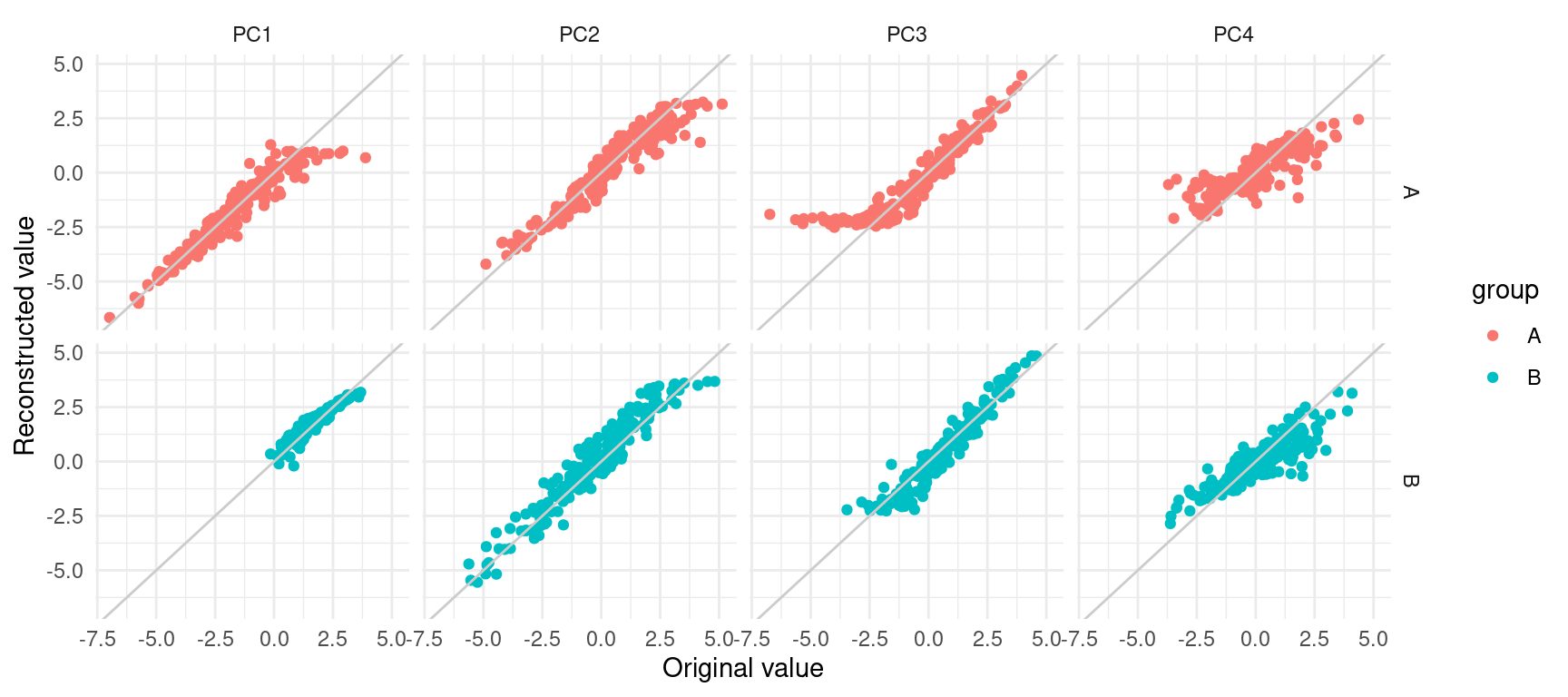

Exemple MNIST

On applique maintenant cette même approche VAE à un jeu de données réel — et très original : MNIST, qui regroupe 70,000 exemples de caractères numériques manuscrits (ie des exemples de digits de 0 à 9). Chaque observation est une image, i.e. une matrice de taille $28\times 28$ où chaque entrée correspond à un niveau de gris quantifié de 0 à 255. On va ici analyser ces données - sans prendre en compte l’aspect “image”: chaque image converti en un vecteur de taille $784$, - sans prendre en compte l’information du label (du digit).

On charge les données à partir du package torchvision et on les reformate

## Chargement des donnees mnist
## Les donnnes vont etre chargees depuis le web  
## et stockees dans le repertoire "dir".
library(torchvision)
dir = './'
x_train <- torchvision::mnist_dataset(
  dir, 
  download = TRUE, 
)

## Processing...
## Done!

## On passe l'echelle de gris en [0,1]
xtrain = x_train$data/255

On peut afficher chaque image:

plot_image <- function(input) {
  par(mar = c(0, 0, 0, 0))
  image(input[28:1,] |> t(), 
        col = gray.colors(256, start = 0, end = 1, rev = FALSE), 
        axes = FALSE)  
}
plot_image(xtrain[3,,])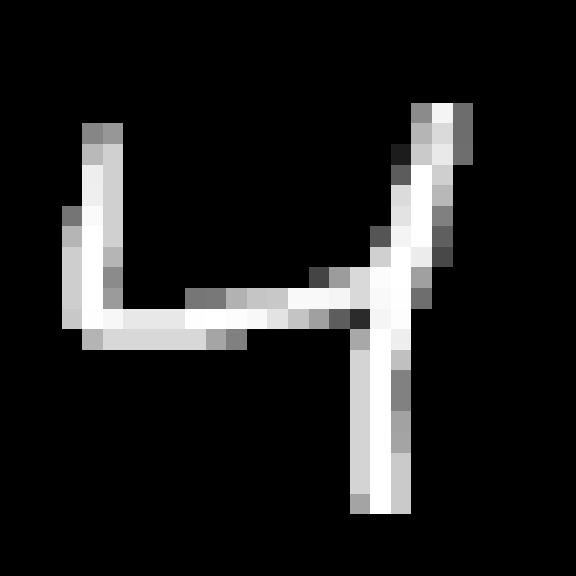

Et on continue le traitement des données:

## On passe les images en vecteur
input_dim = dim(xtrain)[2]*dim(xtrain)[3]
xtrain <- torch_reshape(xtrain, c(nrow(xtrain), input_dim))
dim(xtrain)

## [1] 60000   784

## On recupere les labels
ytrain <- x_train$targets

On choisit la taille de l’espace latent (ici deux pour faciliter les représentations graphiques des données)

latent_dim = 2

Création de l’encodeur

Il sera constitué de 2 couches denses avec fonction d’activation RELU:

## Création d'un module compressor, qui genere un objet nn_module
create_compressor <- function(input_dim) {
  nn_sequential(
    nn_linear(input_dim, 100),
    nn_relu(),
    nn_linear(100, 20),
    nn_relu(),
  )  
}

## Verification
create_compressor(input_dim)

## An `nn_module` containing 80,520 parameters.
## 
## ── Modules ─────────────────────────────────────────────────────────────────────
## • 0: <nn_linear> #78,500 parameters
## • 1: <nn_relu> #0 parameters
## • 2: <nn_linear> #2,020 parameters
## • 3: <nn_relu> #0 parameters

Le résultat issu du compresseur est ensuite utilisé pour générer la moyenne et la variance de la variable latente :

## Création de l'encodeur à l'aide du compresseur
encoder <- nn_module(
  classname = "encoder", 
  ## Définition des couches
  initialize = function(input_dim, latent_dim) {
  self$compressor <- create_compressor(input_dim)
  self$mean <- nn_linear(20, latent_dim)
  self$log_var  <- nn_linear(20, latent_dim)
  }, 
  ## Définitions des calculs
  forward = function(input) {
    ## Calcul des répresentations compressées
    compressed <- self$compressor(input)
    ## Création des paramètres de moyenne et de variance
    mean <- self$mean(compressed)
    log_var <- self$log_var(compressed)
    ## L'encodeur renvoie mean et log_var
    list(mean = mean, log_var = log_var)
  }
)

## Vérification
enc <- encoder(input_dim, latent_dim)
enc(xtrain[1:2, ])

## $mean
## torch_tensor
##  0.0621  0.1230
##  0.0600  0.1309
## [ CPUFloatType{2,2} ][ grad_fn = <AddmmBackward0> ]
## 
## $log_var
## torch_tensor
## -0.0487  0.1908
## -0.0583  0.2027
## [ CPUFloatType{2,2} ][ grad_fn = <AddmmBackward0> ]

Création du décodeur

Le décompresseur est ici le symétrique du compresseur : deux couches denses avec fonction d’activation RELU :

## Création d'un module decompressor
create_decompressor <- function(latent_dim, input_dim) {
  nn_sequential(
    nn_linear(latent_dim, 20),
    nn_relu(),
    nn_linear(20, 100),
    nn_relu(),
    nn_linear(100, input_dim),
  )  
}

## Verif
create_decompressor(latent_dim,input_dim)

## An `nn_module` containing 81,344 parameters.
## 
## ── Modules ─────────────────────────────────────────────────────────────────────
## • 0: <nn_linear> #60 parameters
## • 1: <nn_relu> #0 parameters
## • 2: <nn_linear> #2,100 parameters
## • 3: <nn_relu> #0 parameters
## • 4: <nn_linear> #79,184 parameters

## Création du decodeur à l'aide du decompresseur
decoder <- nn_module(
  classname = "decoder", 
  ## Définition des couches
  initialize = function(latent_dim, input_dim) {
    self$decompressor <- create_decompressor(latent_dim, input_dim)
  }, 
  ## Définitions des calculs
  forward = function(input) {
    self$decompressor(input)
  }
)

## Verif
dec <- decoder(latent_dim, input_dim)
latent_vectors <- matrix(0, nrow = 5, ncol = latent_dim) %>% torch_tensor() 
dec(latent_vectors)

## torch_tensor
## Columns 1 to 10-0.0711 -0.0603  0.0660 -0.0456  0.0687  0.0270  0.0493 -0.0770  0.0530 -0.0106
## -0.0711 -0.0603  0.0660 -0.0456  0.0687  0.0270  0.0493 -0.0770  0.0530 -0.0106
## -0.0711 -0.0603  0.0660 -0.0456  0.0687  0.0270  0.0493 -0.0770  0.0530 -0.0106
## -0.0711 -0.0603  0.0660 -0.0456  0.0687  0.0270  0.0493 -0.0770  0.0530 -0.0106
## -0.0711 -0.0603  0.0660 -0.0456  0.0687  0.0270  0.0493 -0.0770  0.0530 -0.0106
## 
## Columns 11 to 20-0.1359 -0.0175  0.0157 -0.0740  0.1248  0.0710  0.0563 -0.0788 -0.1138  0.0296
## -0.1359 -0.0175  0.0157 -0.0740  0.1248  0.0710  0.0563 -0.0788 -0.1138  0.0296
## -0.1359 -0.0175  0.0157 -0.0740  0.1248  0.0710  0.0563 -0.0788 -0.1138  0.0296
## -0.1359 -0.0175  0.0157 -0.0740  0.1248  0.0710  0.0563 -0.0788 -0.1138  0.0296
## -0.1359 -0.0175  0.0157 -0.0740  0.1248  0.0710  0.0563 -0.0788 -0.1138  0.0296
## 
## Columns 21 to 30 0.0424 -0.0906  0.0860 -0.1267  0.0340 -0.1034  0.0029  0.0399  0.1031 -0.0155
##  0.0424 -0.0906  0.0860 -0.1267  0.0340 -0.1034  0.0029  0.0399  0.1031 -0.0155
##  0.0424 -0.0906  0.0860 -0.1267  0.0340 -0.1034  0.0029  0.0399  0.1031 -0.0155
##  0.0424 -0.0906  0.0860 -0.1267  0.0340 -0.1034  0.0029  0.0399  0.1031 -0.0155
##  0.0424 -0.0906  0.0860 -0.1267  0.0340 -0.1034  0.0029  0.0399  0.1031 -0.0155
## 
## Columns 31 to 40-0.1238  0.0874 -0.0383 -0.0470 -0.0427 -0.0935 -0.0810  0.0893  0.1160 -0.1416
## -0.1238  0.0874 -0.0383 -0.0470 -0.0427 -0.0935 -0.0810  0.0893  0.1160 -0.1416
## -0.1238  0.0874 -0.0383 -0.0470 -0.0427 -0.0935 -0.0810  0.0893  0.1160 -0.1416
## -0.1238  0.0874 -0.0383 -0.0470 -0.0427 -0.0935 -0.0810  0.0893  0.1160 -0.1416
## -0.1238  0.0874 -0.0383 -0.0470 -0.0427 -0.0935 -0.0810  0.0893  0.1160 -0.1416
## 
## Columns 41 to 50-0.1068 -0.0549  0.1539  0.0530  0.0458 -0.0235  0.0238 -0.1271 -0.1127  0.1080
## -0.1068 -0.0549  0.1539  0.0530  0.0458 -0.0235  0.0238 -0.1271 -0.1127  0.1080
## -0.1068 -0.0549  0.1539  0.0530  0.0458 -0.0235  0.0238 -0.1271 -0.1127  0.1080
## -0.1068 -0.0549  0.1539  0.0530  0.0458 -0.0235  0.0238 -0.1271 -0.1127  0.1080
## -0.1068 -0.0549  0.1539  0.0530  0.0458 -0.0235  0.0238 -0.1271 -0.1127  0.1080
## 
## ... [the output was truncated (use n=-1 to disable)]
## [ CPUFloatType{5,784} ][ grad_fn = <AddmmBackward0> ]

Création de l’échantillonneur

vae_sampler <- nn_module(
  classname = "sampler", 
  initialize = function(input_dim, latent_dim) {
    self$latent_dim <- latent_dim
    self$encoder <- encoder(input_dim, latent_dim)
    self$decoder <- decoder(latent_dim, input_dim)
  },
  forward = function(input) {
    ## compression des données
    comp_input <- self$encoder(input)
    mean <- comp_input$mean
    log_var <- comp_input$log_var
    ## échantillonnage dans l'espace latent
    z <- mean + torch_exp(log_var$mul(0.5))*torch_randn(nrow(input), self$latent_dim)
    ## décompression de la représentation latente
    decomp_input <- self$decoder(z)
    
    list(decomp_input = decomp_input, 
         z            = z, 
         mean         = mean, 
         log_var      = log_var)
  }
)
## Verification
vae <- vae_sampler(input_dim, latent_dim)
vae(xtrain[1, , drop = FALSE])

## $decomp_input
## torch_tensor
## Columns 1 to 10-0.0367  0.0152 -0.0754 -0.0464 -0.0218  0.0021 -0.0245 -0.1268 -0.1391 -0.0633
## 
## Columns 11 to 20-0.1127  0.0286  0.1555 -0.0588  0.0952 -0.1028  0.0084 -0.1734  0.0828 -0.0322
## 
## Columns 21 to 30-0.0395  0.0475 -0.1117 -0.0569 -0.1394 -0.0685  0.0260 -0.0435 -0.0292 -0.1345
## 
## Columns 31 to 40 0.0639  0.0315 -0.1756 -0.1320 -0.0080 -0.0549  0.0222 -0.2048 -0.0229  0.0902
## 
## Columns 41 to 50-0.0030  0.0063 -0.0300  0.0031  0.1374 -0.0240  0.1296  0.1182 -0.0757  0.0312
## 
## Columns 51 to 60 0.0533 -0.1802  0.0035 -0.0317 -0.1715  0.1829  0.0638 -0.0043 -0.0538 -0.2379
## 
## Columns 61 to 70 0.0214 -0.0245 -0.0780 -0.2163 -0.0421 -0.0379 -0.0567  0.1672  0.0314 -0.0353
## 
## Columns 71 to 80-0.0437 -0.0381 -0.1976  0.1238 -0.1938  0.0463  0.1006 -0.0311  0.1141 -0.1697
## 
## Columns 81 to 90-0.1109  0.0701  0.1713  0.0538 -0.0208  0.1935 -0.1954 -0.0950  0.1213 -0.0467
## 
## Columns 91 to 100-0.1257  0.1325  0.0209  0.0643  0.1084 -0.0999 -0.0159  0.0007  0.0804 -0.0578
## 
## Columns 101 to 110-0.0427 -0.1312 -0.1068 -0.0707  0.0016  0.0229 -0.0195  0.0591 -0.0028  0.1412
## 
## Columns 111 to 120 0.0297 -0.0214  0.0737  0.0762 -0.1720 -0.0983 -0.0397 -0.0355 -0.0132 -0.0295
## 
## Columns 121 to 130 0.1599 -0.0073 -0.0998 -0.0894  0.0905  0.0031  0.0051 -0.0922  0.0904 -0.0431
## 
## Columns 131 to 140 0.0938  0.0888 -0.1081  0.0200  0.0035  0.0433  0.0267 -0.1272 -0.0368  0.1087
## 
## Columns 141 to 150-0.0294  0.0596  0.1273  0.1266  0.0070  0.0231  0.1186 -0.0297  0.0560  0.0660
## 
## ... [the output was truncated (use n=-1 to disable)]
## [ CPUFloatType{1,784} ][ grad_fn = <AddmmBackward0> ]
## 
## $z
## torch_tensor
## -0.9603 -0.0634
## [ CPUFloatType{1,2} ][ grad_fn = <AddBackward0> ]
## 
## $mean
## torch_tensor
## 0.01 *
## -4.0147 -1.4044
## [ CPUFloatType{1,2} ][ grad_fn = <AddmmBackward0> ]
## 
## $log_var
## torch_tensor
## 0.01 *
## -5.2364 -5.5001
## [ CPUFloatType{1,2} ][ grad_fn = <AddmmBackward0> ]

Optimisation

La méthode d’optimisation choisie est ADAM :

## Definition de l'optimiseur
optimizer_vae <- optim_adam(vae$parameters, lr = 0.001)

et la fonction de perte combine ici MSE (pour le terme d’ajustement) et la pénalité Kullback Leibler :

## Entraînement du VAE
loss_fn <- function(prediction, target, mean, log_var) {
  ## Perte L2 pour la reconstruction 
  cross_entropy <- nn_mse_loss(reduction = "sum")
  #cross_entropy <- nn_cross_entropy_loss(reduction = "sum")
  
  ## KL part of the loss
  kl <- function(mean, log_var) {
    kl_div <- 1 + log_var - mean$square() - log_var$exp()
    kl_div$multiply(-0.5)$sum()
  }
  
  ## Addition des deux 
  cross_entropy(prediction, target) + kl(mean, log_var)  
}
eval_loss <- function(input) {
  target <- input
  
  ## Extraction des composant prediction, mean, log_var depuis le VAE
  results <- vae(input)
  mean <- results$mean
  log_var <- results$log_var
  prediction <- results$decomp_input
  
  loss_fn(prediction, target, mean, log_var)
}

On lance l’optimisation (sur 10,000 observations seulement) :

num_iterations <- 250
loss_vector <- vector("numeric", num_iterations)
for (i in 1:num_iterations) {
  optimizer_vae$zero_grad()
  loss <- eval_loss(xtrain[1:10000,])
  loss$backward()
  loss_vector[i] <- loss %>% as.numeric()
  optimizer_vae$step()
}

On observe l’évolution de la fonction de perte :

plot(loss_vector)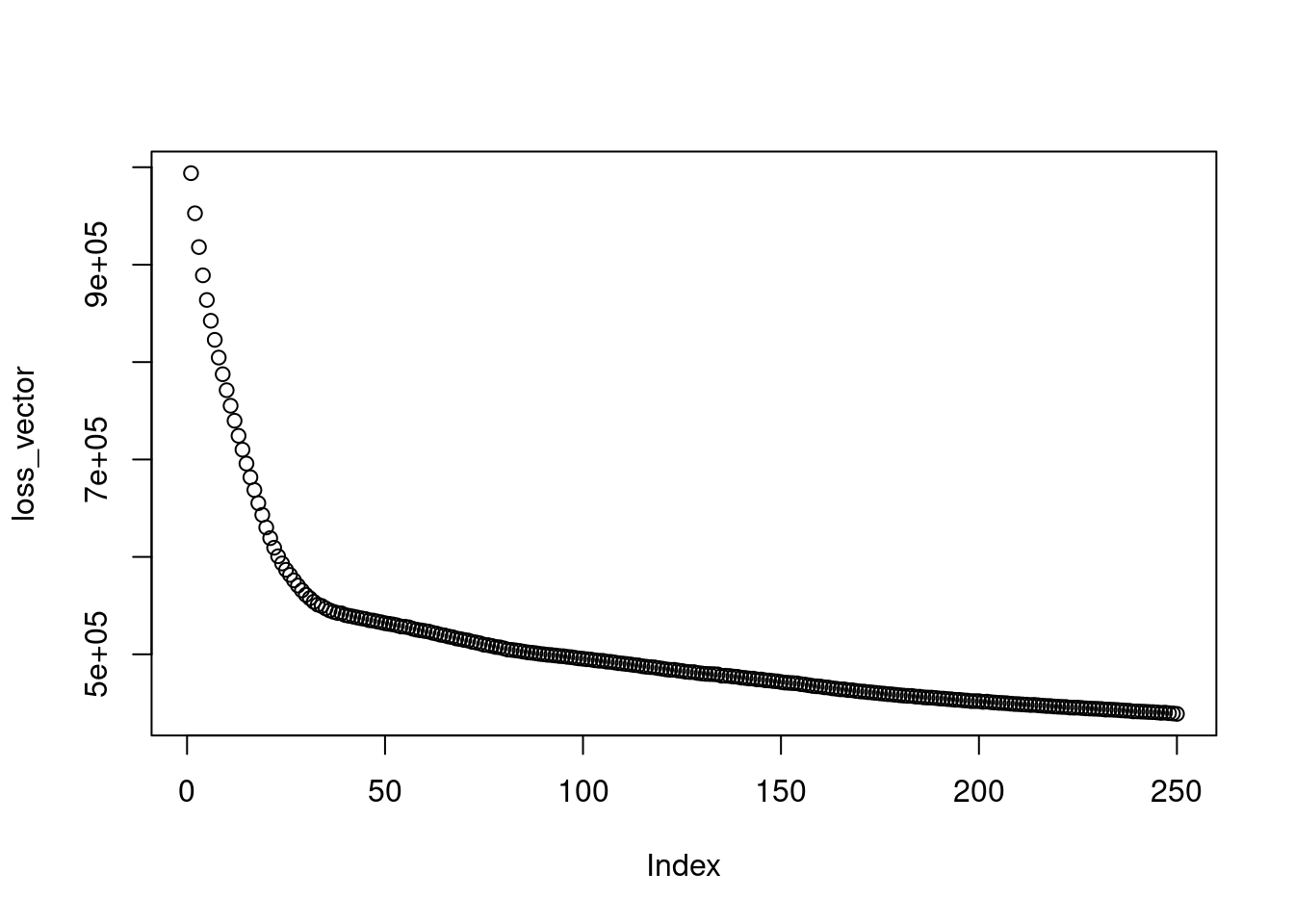

On peut récupérer directement la matrice des moyennes inférées

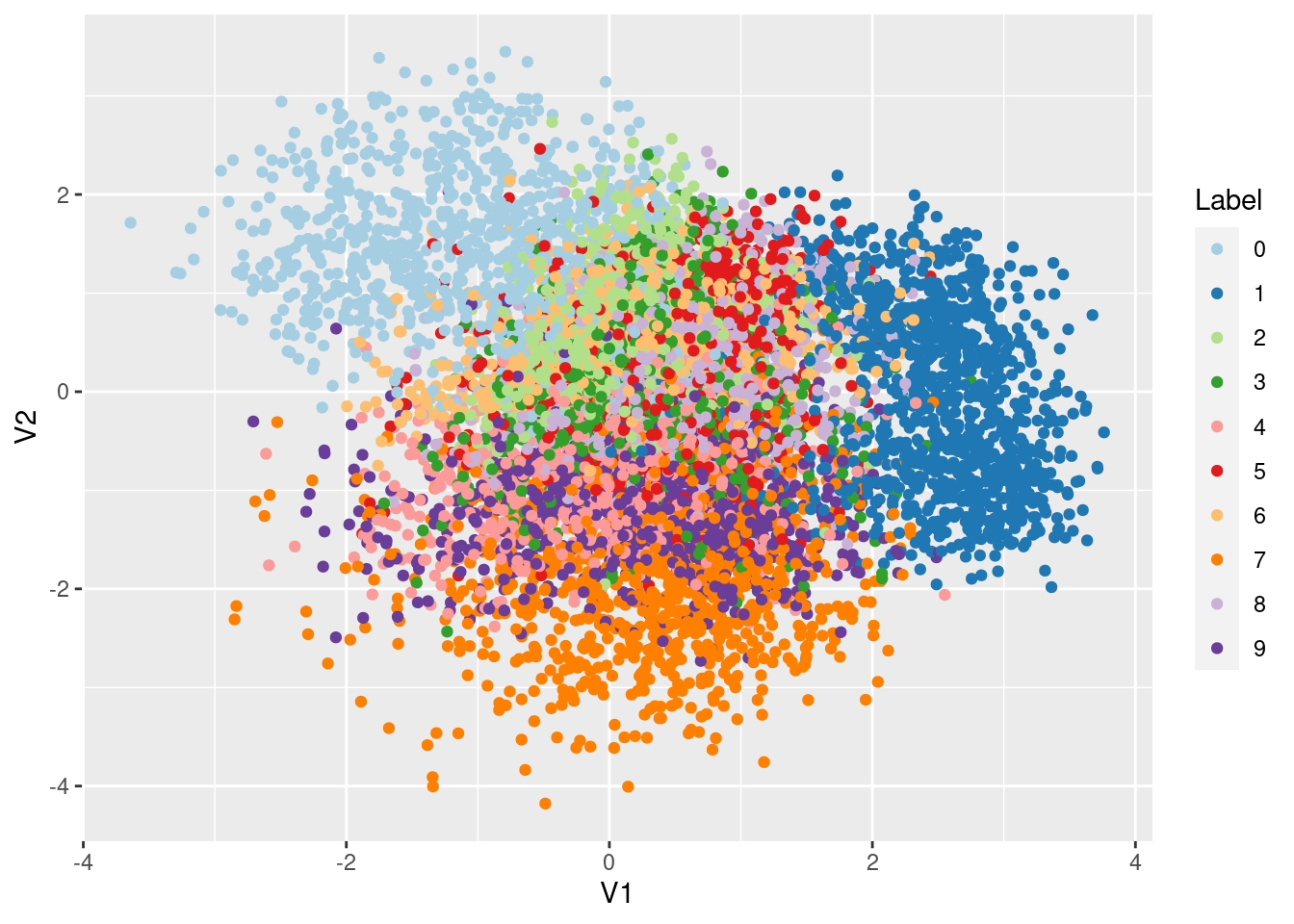
Res1 <- vae$encoder(xtrain[1:10000,])$mean

afin de représenter les données dans l’espace latent

Res1 %>% 
  as.matrix %>% 
  as.data.frame() %>% 
  mutate(Label = as.factor(ytrain[1:10000] - 1L)) %>%
  ggplot(aes(x=V1,y=V2,col=Label)) + geom_point() + 
  scale_color_brewer(palette = "Paired")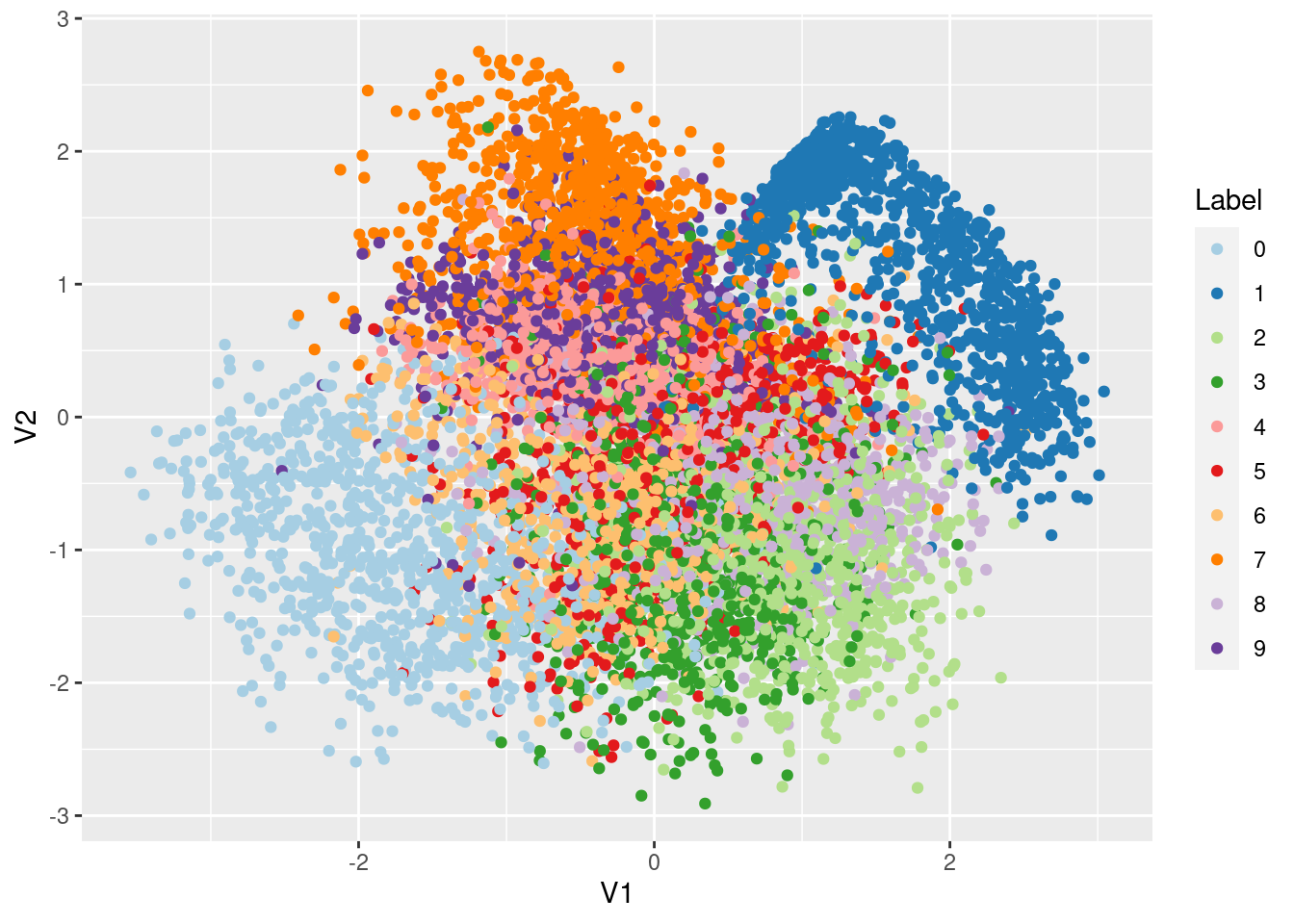

Alternativement, on peut générer la représentation graphique correspondant à un point donné dans l’espace latent :

vae$decoder(c(-2,3) %>% torch_tensor) %>% torch_reshape(c(28,28)) %>% as.matrix() %>% plot_image()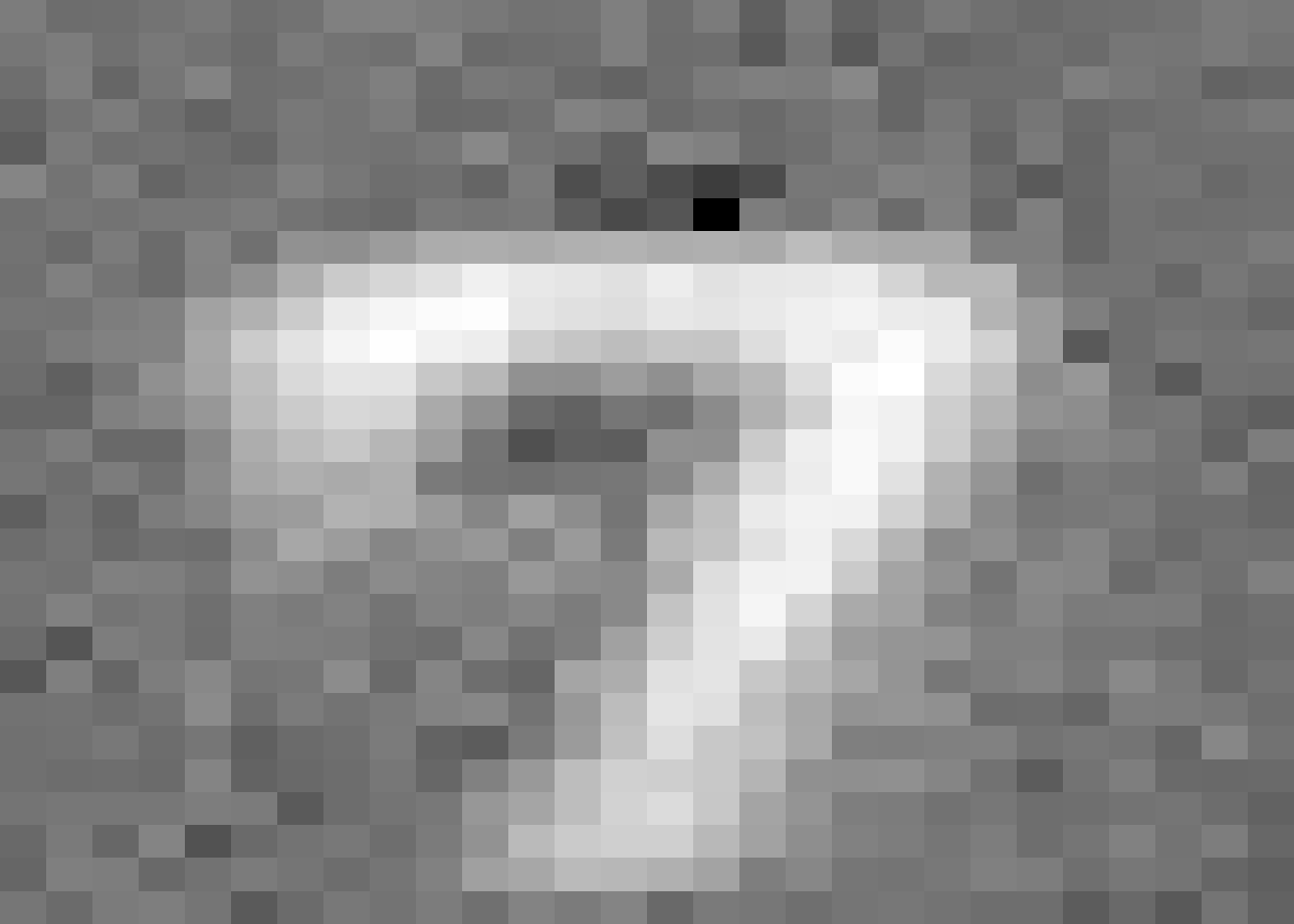

Pour aller plus loin: convolution et mini-batch

On reprend ici l’exemple MNIST en apportant deux nouveautés dans l’analyse : - l’utilisation de réseaux convolutionnels prenant en compte la nature des données. On gardera donc intacte la structure matricielle des données initiales dans ce qui suit; - l’utilisation de batchs lors de l’optimisation. Plutôt que d’utiliser systématiquement l’ensemble des données d’entrainement, on échantillonnera un sous-ensemble de ces données à chaque étape d’optimisation, i.e. on réalisera une descente de gradient stochastique.

L’utilisation d’une procédure d’optimisation stochastique requiert un formattage particulier des données, sous la forme d’un objet de classe dataloader, afin que l’algorithme d’optimisation soit en mesure de réaliser l’échantillonnage à chaque étape.

Le format `dataloader`

On repart du jeu de données formatté xtrain que l’on avait créé dans la section précédente. Le formattage des données en dataloader se fait en deux étapes. La première consiste à mettre les données sous format “dataset” :

## Creation du dataset
mnist.dataset.constructor <- dataset(
  
  name = "mnist_dataset",
  
  initialize = function(input) {
    self$data <- torch_reshape(input, c(dim(input)[1], 1, 28, 28))
  },
  
  .getitem = function(index) {
    self$data[index, ]
  },
  
  .length = function() {
    self$data$size()[[1]]
  }
  
)
mnist.ds <- mnist.dataset.constructor(xtrain[1:10000,])
class(mnist.ds)

## [1] "mnist_dataset" "dataset"       "R6"

L’objet dataset ainsi créé possède en interne une fonction .getitem qui explicite la manière d’extraire une (ou plusieurs) observation(s) dans le jeu de données. Il s’agit de la méthode qui sera appelée par NOM_DU_DATASET[index]. De même, la méthode .length explicite la taille du jeu de données. Ces deux méthodes doivent être définies car elles seront ensuite appelées par le dataloader lors de l’étape de création des batchs. De manière générale, la définition du dataset permet aussi d’inclure une étape de preprocessing des données (ici directement dans la méthode initialize).

En pratique, les données sont stockées dans le membre $data du dataset. On remarque par ailleurs que l’on a au passage reformaté les données : chaque observation est maintenant un array de dimension $1\times28\times28$, i.e une image de taille $28\times28$ décrite par 1 canal. En analyse d’images, le nombre de canaux représente la quantité d’information contenue dans chaque pixel. Par exemple, pour une image en couleurs, il faut 3 canaux : pour le rouge, le bleu et le vert (format RGB), ou pour la luminance et les deux degrés de chrominance (format YCbCr). Ici, pour une image en niveaux de gris, il n’y a qu’un seul canal.

Dans la deuxième étape, on va préciser comment l’on souhaite échantillonner des batchs (i.e. des sous-échantillons) qui seront utilisés lors de l’optimisation. Ici on souhaite que les batchs soient de taille 250 (option batch_size), que la constitution des batchs change à chaque epoch (option shuffle), et que le dernier batch - qui en général est de taille plus petite que les autres lorsque la division du nombre d’observations par la taille d’un batch ne tombe pas rond - soit tout de même utilisé (option drop_last) :

## Definition du dataloader
mnist.dl <- dataloader(mnist.ds, batch_size = 256, shuffle = TRUE, drop_last=FALSE)
mnist.dl$dataset$data %>% dim

## [1] 10000     1    28    28

A chaque itération (epoch) on génère un découpage des données (méthode $.iter()), et pour un découpage donné on peut aller chercher le prochain batch (méthode $.next()). Ce batch est un tenseur dont la taille est celle que l’on attend (ie nb d’obs $\times$ dimension de chaque obs) :

mnist.it = mnist.dl$.iter()
batch = mnist.it$.next()
class(batch)

## [1] "torch_tensor" "R7"

dim(batch)

## [1] 256   1  28  28

Il est aussi possible d’obtenir le nombre de batchs constituant une epoch :

mnist.it$.length()

## [1] 40

Maintenant que les données sont sous le format attendu, on définit le réseau de neurones VAE que l’on souhaite appliquer en suivant les mêmes étapes que dans la section précédente :

## Choix de la dimension latente 
latent_dim <- 2

## Definition de l'encodeur 
encoder.constructor <- nn_module(
  
    name = "encoder",
  
    ## Définition des couches
    initialize = function(latent_dim) {
        self$conv1 = nn_conv2d(1, 4, kernel_size = 3, stride = 1, padding = 0)
        self$conv2 = nn_conv2d(4, 8, kernel_size = 3, stride = 1, padding = 0)
        self$linear = nn_linear(1152, 256)
        self$dropout1 = nn_dropout(.25)
        self$dropout2 = nn_dropout(.25)
        self$mean = nn_linear(256, latent_dim)
        self$log_var = nn_linear(256, latent_dim)
    }, 
    ## Définitions des calculs
    forward = function(input) {
        input = input %>%                                   # N x 1 x 28 x 28
            self$conv1() %>%                                # N x 4 x 26 x 26
            nnf_relu() %>% 
            self$conv2() %>%                                # N x 8 x 24 x 24
            nnf_relu() %>% 
            nnf_max_pool2d(2) %>%                           # N x 8 x 12 x 12
            self$dropout1() %>%
            torch_flatten(start_dim = 2) %>%                # N x 1152
            self$linear() %>%                               # N x 256
            nnf_relu() %>% 
            self$dropout2()
        ## Création des paramètres de moyenne et de variance
        mean <- self$mean(input)                            # N x latent_dim
        log_var <- self$log_var(input)                      # N x latent_dim
        ## L'encodeur renvoie mean et sd
        list(mean    = mean, 
             log_var = log_var)
    }
  
)

On peut vérifier que tout fonction en utilisant un batch de données :

encoder <- encoder.constructor(latent_dim)
encoder

## An `nn_module` containing 296,532 parameters.
## 
## ── Modules ─────────────────────────────────────────────────────────────────────
## • conv1: <nn_conv2d> #40 parameters
## • conv2: <nn_conv2d> #296 parameters
## • linear: <nn_linear> #295,168 parameters
## • dropout1: <nn_dropout> #0 parameters
## • dropout2: <nn_dropout> #0 parameters
## • mean: <nn_linear> #514 parameters
## • log_var: <nn_linear> #514 parameters

verif.e <- encoder(batch)
names(verif.e)

## [1] "mean"    "log_var"

Même chose pour le décodeur

decoder.constructor <- nn_module(
    
    name = "decoder",
  
    ## Définition des couches
    initialize = function(latent_dim) {
        self$linear1 = nn_linear(latent_dim, 256)
        self$linear2 = nn_linear(256, 1152)
        self$unflatten = nn_unflatten(2, c(8, 12, 12))
        self$convt1 = nn_conv_transpose2d(8, 4, kernel_size = 3, stride = 2, padding = 1, output_padding = 1)
        self$convt2 = nn_conv_transpose2d(4, 2, kernel_size = 3, stride = 1, output_padding = 0)
        self$convt3 = nn_conv_transpose2d(2, 1, kernel_size = 3, stride = 1, output_padding = 0)
    }, 
    ## Définitions des calculs
    forward = function(input) {
        input = input %>%                           # N x latent_dim
            self$linear1() %>%                      # N x 256
            nnf_relu() %>% 
            self$linear2() %>%                      # N x 1152
            nnf_relu() %>% 
            self$unflatten() %>%                    # N x 8 x 12 x 12
            self$convt1() %>%                       # N x 4 x 24 x 24
            nnf_relu() %>% 
            self$convt2() %>%                       # N x 2 x 26 x 26
            nnf_relu() %>% 
            self$convt3() %>%                       # N x 1 x 28 x 28
            nnf_sigmoid()        
        input
    }
  
)

decoder <- decoder.constructor(latent_dim)
verif.d <- decoder(verif.e$mean)
dim(verif.d)

## [1] 256   1  28  28

Enfin on définit l’échantillonneur VAE :

## Definition du module VAE
vae_constructor <- nn_module(
  
  initialize = function(latent_dim=10) {
    
    self$latent_dim = latent_dim
    self$encoder <- encoder.constructor(latent_dim)
    self$decoder <- decoder.constructor(latent_dim)
    
  },
  
  forward = function(x) {
    f <- self$encoder(x)
    mu <- f$mean
    log_var <- f$log_var
    z <- mu + torch_exp(log_var$mul(0.5))*torch_randn(c(dim(x)[1], self$latent_dim))
    reconst_x <- self$decoder(z)
    
    list(pred=reconst_x, mean=mu, log_var=log_var)
  }
  
)

## Initialization du VAE 
vae <- vae_constructor(latent_dim=latent_dim)
vae(batch) %>% dim

## NULL

On peut maintenant préciser les modalités de l’optimisation

## Defiition de l'optimiseur
optimizer <- optim_adam(vae$parameters, lr = 0.001)

## Choix du nombre d'epochs
epochs = 10

et lancer l’optimisation. Celle-ci consiste maintenant en une double boucle: dans la première boucle on réalise à chaque étape un découpage du jeu de données en batchs, et dans la deuxième on réalise à chaque étape un pas de descente de gradient calculé avec les données du batch courant. La deuxième boucle nécessite l’instruction loop du package coro qui réalise automatiquement l’itération sur les batchs:

## Boucle for classique sur les epochs
loss.epoch <- rep(0,epochs)
for(epoch in 1:epochs) {
  cat("Epoch #", epoch, ": ", sep = "")
  
  ## Boucle for "coro" pour itérer sur les batchs
  coro::loop(for (minibatch in mnist.dl) {  
    
    forward = vae(minibatch)
    
    ## Calcul de la vraisemblance
    loss = nn_bce_loss(reduction = "sum")
    
    ## Calcul de la pénalité KL
    mu = forward$mean
    log_var = forward$log_var
    kl_div =  1 + log_var - mu$pow(2) - log_var$exp()
    kl_div_sum = - 0.5 *kl_div$sum()
    
    ## Perte à cette étape
    output <- loss(forward$pred, minibatch) + 2 * kl_div_sum
    
    ## On cumule les pertes des batchs pour obtenir in fine celle de l'epoch  
    loss.epoch[epoch] = loss.epoch[epoch] + as.numeric(output)
    # 
    optimizer$zero_grad()
    output$backward()
    optimizer$step()
    
  })
  
  cat(sprintf("Loss = %1f\n", loss.epoch[epoch]))
}

## Epoch #1: Loss = 3916593.846191
## Epoch #2: Loss = 2683816.228027
## Epoch #3: Loss = 2312739.142578
## Epoch #4: Loss = 2157263.294678
## Epoch #5: Loss = 2077953.728516
## Epoch #6: Loss = 1994925.761230
## Epoch #7: Loss = 1932130.208984
## Epoch #8: Loss = 1896283.493652
## Epoch #9: Loss = 1871756.576660
## Epoch #10: Loss = 1853997.068848

A noter qu’il est également possible d’effectuer de l’optimisation par batchs manuellement, sans passer par un dataloader. Il faut en ce cas définir dans la boucle comment s’effectue le choix des batchs.

for (epoch in 1:num_epochs) {
    cat("Epoch #", epoch, ": ", sep = "")
    rand_sample = sample(nrow(xtrain)) # Génère une permutation de [1:n]
    for (iter in 1:240) {               # batch size of 250 for n = 60000
        if (iter %% 10 == 0) cat(iter, ", ", sep = "")
        istart = (iter-1)*250 + 1
        iend = iter*250
        batch_sample = rand_sample[istart:iend]
        output <- loss(forward$pred, xtrain[batch_sample, ]) + kl_div_sum
        [...]
    }
    cat(".\nLoss = ", loss_vector[epoch], ".\n", sep = "")
}

Res1 <- vae$encoder(mnist.dl$dataset$data)$mean

afin de représenter les données dans l’espace latent

Res1 %>% 
  as.matrix %>% 
  as.data.frame() %>% 
  mutate(Label = as.factor(ytrain[1:10000] - 1L)) %>%
  ggplot(aes(x=V1,y=V2,col=Label)) + geom_point() + 
  scale_color_brewer(palette = "Paired")

VAE

finister2022

2023-01-04

Example simple (données mutivariées, sans structures)

Simulation de données

Définition d’un encodeur

Définition d’un décodeur

Définition du VAE

Création du VAE et de l’optimiseur

Entraînement du VAE

Exploration des résultats

Exemple MNIST

Création de l’encodeur

Création du décodeur

Création de l’échantillonneur

Optimisation

Pour aller plus loin: convolution et mini-batch

Le format `dataloader`

VAE

finister2022

2023-01-04

Example simple (données mutivariées, sans structures)

Simulation de données

Définition d’un encodeur

Définition d’un décodeur

Définition du VAE

Création du VAE et de l’optimiseur

Entraînement du VAE

Exploration des résultats

Exemple MNIST

Création de l’encodeur

Création du décodeur

Création de l’échantillonneur

Optimisation

Pour aller plus loin: convolution et mini-batch

Le format dataloader

Le format `dataloader`